题目内容
三棱锥S-ABC中,底面为边长为6的等边三角形,SA=SB=SC,三棱锥的高为
,则侧面与底面所成的二面角为( )
| 3 |
| A.45° | B.30° | C.60° | D.65° |
如图所示,过点S作SO⊥底面ABC,点O为垂足,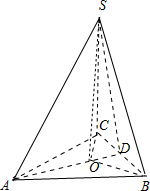
连接OA、OB、OC,则Rt△OAB≌Rt△OBC≌Rt△OCA,∴OA=OB=OC,
∴点O为等边△ABC的中心.
延长AO交BC于点D,连接SD.
则AD⊥BC,再根据三垂线定理可得BC⊥SD.
∴∠ODS为侧面SBC与底面ABC所成的二面角的平面角.
根据重心定理可得:OD=
AD=
×
×6=
.
在Rt△SOD中,tan∠ODS=
=
=1,∴∠ODS=45°.
∴侧面SBC与底面ABC所成的二面角的平面角为45°.
故选A.

连接OA、OB、OC,则Rt△OAB≌Rt△OBC≌Rt△OCA,∴OA=OB=OC,
∴点O为等边△ABC的中心.
延长AO交BC于点D,连接SD.
则AD⊥BC,再根据三垂线定理可得BC⊥SD.
∴∠ODS为侧面SBC与底面ABC所成的二面角的平面角.
根据重心定理可得:OD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
在Rt△SOD中,tan∠ODS=
| SO |
| OD |
| ||
|
∴侧面SBC与底面ABC所成的二面角的平面角为45°.
故选A.

练习册系列答案
相关题目