题目内容
已知函数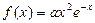 ,
,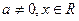 .
.
(I)讨论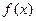 的单调性.
的单调性.
(II)当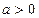 时,讨论关于
时,讨论关于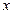 的方程
的方程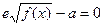 的实根的个数.
的实根的个数.
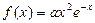 ,
,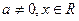 .
.(I)讨论
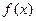 的单调性.
的单调性.(II)当
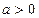 时,讨论关于
时,讨论关于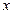 的方程
的方程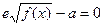 的实根的个数.
的实根的个数.(I)当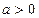 时,
时,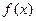 在
在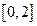 上单调递增,在
上单调递增,在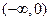 和
和 上单调递减. 当
上单调递减. 当 时,
时,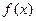 在
在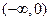 和
和 上单调递增,在
上单调递增,在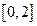 上单调递减(II)即
上单调递减(II)即 时,原方程有一解.
时,原方程有一解. 时,原方程有两解.
时,原方程有两解.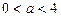 时,原方程有三解.
时,原方程有三解.
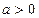 时,
时,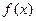 在
在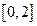 上单调递增,在
上单调递增,在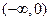 和
和 上单调递减. 当
上单调递减. 当 时,
时,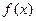 在
在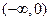 和
和 上单调递增,在
上单调递增,在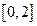 上单调递减(II)即
上单调递减(II)即 时,原方程有一解.
时,原方程有一解. 时,原方程有两解.
时,原方程有两解.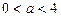 时,原方程有三解.
时,原方程有三解. (I)依题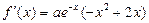 , ―――――――――――――――(1分)
, ―――――――――――――――(1分)
令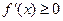 ,即:
,即: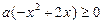 . ―――――――――――――――――――(2分)
. ―――――――――――――――――――(2分)
易知,当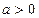 时,
时,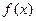 在
在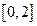 上单调递增, ―――――――――――――――(4分)
上单调递增, ―――――――――――――――(4分)
在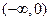 和
和 上单调递减. ――――――――――――――――――(6分)
上单调递减. ――――――――――――――――――(6分)
当 时,
时,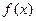 在
在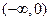 和
和 上单调递增, ――――――――――――(7分)
上单调递增, ――――――――――――(7分)
在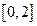 上单调递减. ―――――――――――――――――――――――――-(8分)
上单调递减. ―――――――――――――――――――――――――-(8分)
(II)由(I)知当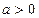 时,
时,
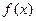 极小=
极小= ,
,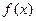 极大=
极大= ――――――――――――――――(9分)
――――――――――――――――(9分)
又当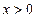 或
或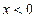 时,
时, ,
,
可见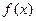 的图象如下: ――――――――――(10分)
的图象如下: ――――――――――(10分)
而方程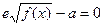 ,
,
转化为 ――――――――――――(11分)
――――――――――――(11分)
可见,当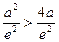 时,即
时,即 时,原方程有一解.
时,原方程有一解.
同理:
 时,原方程有两解.
时,原方程有两解.
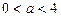 时,原方程有三解. ――――――――-(12分
时,原方程有三解. ――――――――-(12分

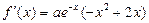 , ―――――――――――――――(1分)
, ―――――――――――――――(1分)令
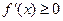 ,即:
,即: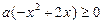 . ―――――――――――――――――――(2分)
. ―――――――――――――――――――(2分)易知,当
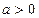 时,
时,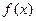 在
在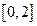 上单调递增, ―――――――――――――――(4分)
上单调递增, ―――――――――――――――(4分)在
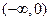 和
和 上单调递减. ――――――――――――――――――(6分)
上单调递减. ――――――――――――――――――(6分)当
 时,
时,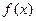 在
在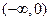 和
和 上单调递增, ――――――――――――(7分)
上单调递增, ――――――――――――(7分)在
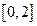 上单调递减. ―――――――――――――――――――――――――-(8分)
上单调递减. ―――――――――――――――――――――――――-(8分)(II)由(I)知当
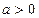 时,
时,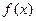 极小=
极小= ,
,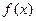 极大=
极大= ――――――――――――――――(9分)
――――――――――――――――(9分)又当
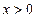 或
或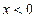 时,
时, ,
,可见
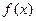 的图象如下: ――――――――――(10分)
的图象如下: ――――――――――(10分)而方程
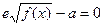 ,
,转化为
 ――――――――――――(11分)
――――――――――――(11分)可见,当
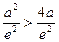 时,即
时,即 时,原方程有一解.
时,原方程有一解.同理:
 时,原方程有两解.
时,原方程有两解.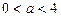 时,原方程有三解. ――――――――-(12分
时,原方程有三解. ――――――――-(12分

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (x)= ( )
(x)= ( )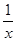 +1
+1  满足
满足 ,则
,则


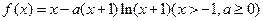 .
.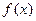 的单调区间;
的单调区间;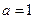 时,若方程
时,若方程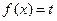 在
在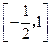 上有两个实数解,求实数
上有两个实数解,求实数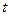 的取值范围;
的取值范围;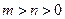 时,
时,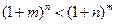 .
.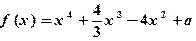
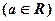
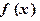 的极大值;
的极大值;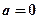 时,求函数
时,求函数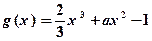 ,当
,当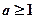 时,
时,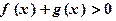 恒成立,求
恒成立,求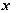 的取值范围.
的取值范围.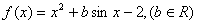 ,且对任意
,且对任意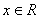 ,有
,有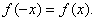
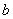 。
。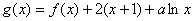 在区间(0,1)上为单调函数,求实数
在区间(0,1)上为单调函数,求实数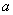 的取值范围。
的取值范围。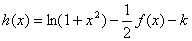 的零点个数?
的零点个数?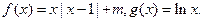 (1)当
(1)当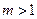 时,求函数
时,求函数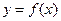 在
在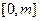 上的最大值;(2)记函数
上的最大值;(2)记函数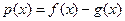 ,若函数
,若函数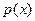 有零点,求
有零点,求 的取值范围.
的取值范围.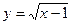 ,则它的导函数是 ( )
,则它的导函数是 ( )



 的解析式可能是( )
的解析式可能是( )


