题目内容
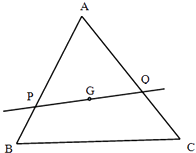
【题目】设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若 ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() .
. 
(1)求 ![]() 的值;
的值;
(2)求λμ的取值范围.
【答案】
(1)解:连接AG并延长,交BC于M,则M是BC的中点,设 ![]() ,
, ![]() ,
,
![]() ,
,
![]()
∴ ![]() .
.
∵P,G,Q三点共线,故存在实数t,使 ![]() ,
,
∴ 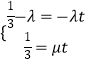 ,
,
∴ ![]() ;
;
(2)解:由(1)得μ= ![]() ,
,
∵λ,μ∈(0,1),∴ 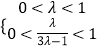 ,解得
,解得 ![]() <λ<1.∴1<
<λ<1.∴1< ![]() .
.
∴λμ= ![]() =
= ![]() =
= ![]() .
.
∴当 ![]() 时,λμ取得最小值
时,λμ取得最小值 ![]() ,当
,当 ![]() =1或2时,λμ取得最大值
=1或2时,λμ取得最大值 ![]() .
.
∴λμ的取值范围是[ ![]() ,
, ![]() ).
).
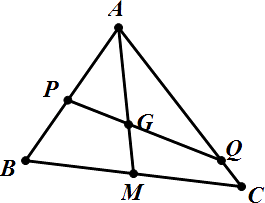
【解析】(1)用 ![]() ,
, ![]() 表示出
表示出 ![]() ,
, ![]() ,根据P,Q,G三点共线得出λ,μ的关系;(2)用λ表示出μ,令λ,μ∈(0,1)得出λ的范围,则λμ可表示为关于λ的函数,求出该函数的最值即可.
,根据P,Q,G三点共线得出λ,μ的关系;(2)用λ表示出μ,令λ,μ∈(0,1)得出λ的范围,则λμ可表示为关于λ的函数,求出该函数的最值即可.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】《中国诗词大会》是中央电视台最近新推出的一档有重大影响力的大型电视文化节目,今年两会期间,教育部部长陈宝生答记者问时给予其高度评价。基于这样的背景,山东某中学积极响应,也举行了一次诗词竞赛。组委会在竞赛后,从中抽取了100名选手的成绩(百分制),作为样本进行统计,作出了图中的频率分布直方图,分析后将得分不低于60分的学生称为“诗词达人”,低于60分的学生称为“诗词待加强者”.

(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否在犯错误的概率不超过0.01的前提下认为“诗词达人”与性别有关?
诗词待加强者 | 诗词达人 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
(Ⅱ)将频率视为概率,现在从该校大量参与活动的学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“诗词达人”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |