题目内容
已知数列![]() 满足:
满足: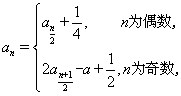 (
(![]() 为常数),
为常数),
数列![]() 中,
中,![]() 。
。
(1)求![]() ;
;
(2)证明:数列![]() 为等差数列;
为等差数列;
(3)求证:数列![]() 中存在三项构成等比数列时,
中存在三项构成等比数列时,![]() 为有理数。
为有理数。
解:⑴由已知![]() ,得
,得![]() ,
,
![]() ,
,![]() 。 ……………………4分
。 ……………………4分
⑵![]() ,
,
![]()
∴![]() ,又
,又![]() ,
,
∴数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列。……………………9分
的等差数列。……………………9分
⑶证明:由⑵知![]() , ……………………10分
, ……………………10分
若三个不同的项![]() 成等比数列,、
成等比数列,、![]() 、
、![]() 为非负整数,且
为非负整数,且![]() ,
,
则![]() ,得
,得![]() , ……………………12分
, ……………………12分
若![]() ,则
,则![]() ,得=
,得=![]() =
=![]() ,这与
,这与![]() 矛盾。 ………………14分
矛盾。 ………………14分
若![]() ,则
,则![]() ,∵
,∵![]() 、
、![]() 、
、![]() 为非负整数,∴
为非负整数,∴![]() 是有理数。……16分
是有理数。……16分

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 依次是等比数列
依次是等比数列 的前两项。
的前两项。
 且
且 ,使得数列
,使得数列 是常数列?若存在,求出
是常数列?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。