题目内容
(2012•梅州二模)己知椭圆C:
+
=1(a>b>0)的离心率为
,不等式
+
≤1所表示的平面区域的面积为16
.
(1)求椭圆C的方程;
(2)设椭圆C的左项点为A,上顶点为B,圆M过A、B两点.当圆心M与原点O的距离最小时,求圆M的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
(1)求椭圆C的方程;
(2)设椭圆C的左项点为A,上顶点为B,圆M过A、B两点.当圆心M与原点O的距离最小时,求圆M的方程.
分析:(1)利用椭圆C的离心率为
,可得a=
b,根据不等式
+
≤1所表示的平面区域的面积为16
,可得4×
ab=16
,由此可求得a,b的值,从而可得椭圆C的方程;
(2)确定AB的垂直平分线L的方程,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程,联立可得M的坐标与圆的半径,从而可得圆M的方程.
| ||
| 2 |
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
| 1 |
| 2 |
| 2 |
(2)确定AB的垂直平分线L的方程,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程,联立可得M的坐标与圆的半径,从而可得圆M的方程.
解答:解:(1)∵椭圆C:
+
=1(a>b>0)的离心率为
,∴
=
∴a=
b①
根据对称性,可得不等式
+
≤1所表示的平面区域是椭圆C的四个顶点为顶点的菱形
∵不等式
+
≤1所表示的平面区域的面积为16
.
∴4×
ab=16
②
由①②解得a=4,b=2
∴椭圆C的方程为
+
=1;
(2)由题意,A(-4,0),B(0,2
),可得AB的垂直平分线L的方程为:
x+y+
=0
点M在L上,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程为:y=
x
解方程组
得x=-
,y=-
∴M(-
,-
),此时r2=
∴圆M的方程为(x+
)2+(y+
)2=
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| a |
| ||
| 2 |
∴a=
| 2 |
根据对称性,可得不等式
| |x| |
| a |
| |y| |
| b |
∵不等式
| |x| |
| a |
| |y| |
| b |
| 2 |
∴4×
| 1 |
| 2 |
| 2 |
由①②解得a=4,b=2
| 2 |
∴椭圆C的方程为
| x2 |
| 16 |
| y2 |
| 8 |
(2)由题意,A(-4,0),B(0,2
| 2 |
| 2 |
| 2 |
点M在L上,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程为:y=
| ||
| 2 |
解方程组
|
| 2 |
| 3 |
| ||
| 3 |
∴M(-
| 2 |
| 3 |
| ||
| 3 |
| 102 |
| 9 |
∴圆M的方程为(x+
| 2 |
| 3 |
| ||
| 3 |
| 102 |
| 9 |
点评:本题考查椭圆的标准方程,考查圆的方程,确定圆的圆心与半径是关键.

练习册系列答案
相关题目
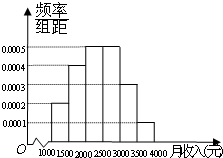 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).