题目内容
(2012•梅州二模)定义在R上的函数f(x)满足:f(x+y)=f(x)f(y),且当x>0时,f(x)>1.
(1)求f(0)的值,并证明f(x)是定义域上的增函数:
(2)数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)(n=1,2,3,…),求数列{an}的通项公式及前n项和Sn.
(1)求f(0)的值,并证明f(x)是定义域上的增函数:
(2)数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)(n=1,2,3,…),求数列{an}的通项公式及前n项和Sn.
分析:(1)在 f(x+y)=f(x)f(y)中,令 x=1,y=0,可得f(0)=1,可以退出当x∈R时,f(x)>0.设x1<x2,计算 f(x1)-f(x2)<0,可得f(x)是定义域上的增函数.
(2)由数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)=f[(aan)+(a-1)],由f(x)是定义域R上的增函数,可得 an+1+1=a(an +1),故{an +1}是以a+1为首项,以a为公比的等比数列.求出{an +1}的通项公式可得{an }的通项公式,从而求得{an }的前n项和sn.
(2)由数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)=f[(aan)+(a-1)],由f(x)是定义域R上的增函数,可得 an+1+1=a(an +1),故{an +1}是以a+1为首项,以a为公比的等比数列.求出{an +1}的通项公式可得{an }的通项公式,从而求得{an }的前n项和sn.
解答:解:(1)在 f(x+y)=f(x)f(y)中,令 x=1,y=0,可得f(1)=f(1)f(0).再由f(1)>1,可得f(0)=1.
当x<0时,f(x-x)=f(0)=f(x)f(-x)=1,由-x>0 可得f(-x)>1,f(x)=
∈(0,1).
当x>0时,同理可得f(x)>0. 综上可得,当x∈R时,f(x)>0.
设x1<x2,则 f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)f(x2)-f(x2)=f(x2)[f(x1-x2)-1].
由x1-x2<0,x<0时,0<f(x)<1,可得 f(x1-x2)-1<0,
∴f(x1)-f(x2)<0,f(x1)<f(x2),
故f(x)是定义域上的增函数.
(2)数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)=f[(aan)+(a-1)],
由f(x)是定义域R上的增函数,可得an+1=aan +a-1,即an+1+1=a(an +1),故{an +1}是以a+1为首项,以a为公比的等比数列.
故 an +1=(a+1)an-1,故 an =(a+1)an-1-1.
故{an }的前n项和sn=(a+1)(1+a+a2+a3+…+an-1)-n=
.
当x<0时,f(x-x)=f(0)=f(x)f(-x)=1,由-x>0 可得f(-x)>1,f(x)=
| 1 |
| f(-x) |
当x>0时,同理可得f(x)>0. 综上可得,当x∈R时,f(x)>0.
设x1<x2,则 f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)f(x2)-f(x2)=f(x2)[f(x1-x2)-1].
由x1-x2<0,x<0时,0<f(x)<1,可得 f(x1-x2)-1<0,
∴f(x1)-f(x2)<0,f(x1)<f(x2),
故f(x)是定义域上的增函数.
(2)数列{an}满足a1=a≠0,f(an+1)=f(aan)f(a-1)=f[(aan)+(a-1)],
由f(x)是定义域R上的增函数,可得an+1=aan +a-1,即an+1+1=a(an +1),故{an +1}是以a+1为首项,以a为公比的等比数列.
故 an +1=(a+1)an-1,故 an =(a+1)an-1-1.
故{an }的前n项和sn=(a+1)(1+a+a2+a3+…+an-1)-n=
|
点评:本题主要考查函数的单调性的应用,等比数列的通项公式,等比数列的前n项和公式的应用,属于中档题.

练习册系列答案
相关题目
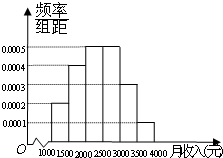 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).