题目内容
(2012•梅州二模)设b,c表示两条直线,α,β表示两个平面,则下列为真命题的是( )
分析:先利用直线与平面的位置关系:直线与平面平行、直线与平面相交、直线在平面内,排除A、B、D,再利用线面平行的性质定理和面面垂直的判定定理证明C为真命题
解答:解:
⇒b∥c或b、c异面,排除A;
⇒c∥α或c?α,排除B;
⇒c⊥β或c∥β或c?β,排除D;
⇒在平面α内存在直线c′∥c,且c′⊥β,由面面垂直的判定定理知C正确;
故选C
|
|
|
|
故选C
点评:本题主要考查了线面平行的位置关系和定义,空间直线与平面位置关系的判定,面面垂直的判定定理,空间想象能力,属基础题

练习册系列答案
相关题目
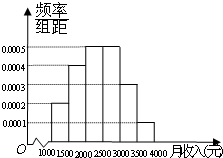 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).