题目内容
12.对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a.f1(x)+b.f2(x),那么称h(x)为f1(x),f2(x)的线性函数.(1)下面给出两组函数,h(x)是否分别为f1(x),f2(x),的线性函数?并说明理由;
第一组:f1(x)=lg$\frac{x}{10}$,f2(x)=lg10x,h(x)=lgx,;
第二组:f1(x)=x2-x,f2(x)=x2+x+1,h(x)=x2-x+1;
(2)设f1(x)=log2x,f2(x)=log${\;}_{\frac{1}{2}}$x,a=2,b=1,线性函数h(x).若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,求实数t的取值范围.
分析 (1)①设alg$\frac{x}{10}$+blg10x=lgx,从而得$\left\{\begin{array}{l}{a+b=1}\\{a-b=0}\end{array}\right.$;从而判断;
②设a(x2-x)+b(x2+x+1)=x2-x+1,从而得$\left\{\begin{array}{l}{a+b=1}\\{b-a=-1}\\{b=1}\end{array}\right.$,从而判断;
(2)化简h(x)=2log2x+log${\;}_{\frac{1}{2}}$x=log2x,从而为t<-(3h2(x)+2h(x))=-3log22x-2log2x,再设s=log2x,则s∈[1,2],从而得y=-3s2-2s,从而化为最值问题.
解答 解:(1)①设alg$\frac{x}{10}$+blg10x=lgx,
则$\left\{\begin{array}{l}{a+b=1}\\{a-b=0}\end{array}\right.$;
解得,a=b=$\frac{1}{2}$;
所以h(x)是f1(x),f2(x)的线性函数;
②设a(x2-x)+b(x2+x+1)=x2-x+1,
即(a+b)x2+(b-a)x+b=x2-x+1,
则$\left\{\begin{array}{l}{a+b=1}\\{b-a=-1}\\{b=1}\end{array}\right.$,
该方程组无解;
所以h(x)不是f1(x),f2(x)的线性函数.
(2)h(x)=2log2x+log${\;}_{\frac{1}{2}}$x=log2x,
若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,
即t<-(3h2(x)+2h(x))=-3log22x-2log2x,
设s=log2x,则s∈[1,2],
y=-3log22x-2log2x=-3s2-2s,
则ymax=-5,
故,t<-5.
点评 本题考查了学生对新定义的接受与应用能力,同时考查了存在性问题及最值问题,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
| A. | 20 | B. | 12 | C. | 8 | D. | 4 |
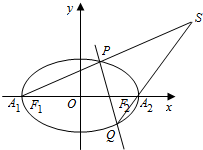 如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S.
如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S. 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为$\frac{1}{2}$
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为$\frac{1}{2}$