题目内容
12.对于大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”:23=3+5,33=7+9+11,43=13+15+17+19,…,仿此,若m3的“分裂数”中有一个是61,则m的值是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由题意知,n的三次方就是n个连续奇数相加,且从2开始,这些三次方的分解正好是从奇数3开始连续出现,由此规律即可找出m3的“分裂数”中有一个是61时,m的值.
解答 解:由题意,从23到m3,正好用去从3开始的连续奇数共2+3+4+…+m=$\frac{(m+2)(m-1)}{2}$个,
61是从3开始的第30个奇数
当m=7时,从23到73,用去从3开始的连续奇数共$\frac{(7+2)(7-1)}{2}$=27个
当m=8时,从23到83,用去从3开始的连续奇数共$\frac{(8+2)(8-1)}{2}$=35个
所以m=8
故选:C.
点评 本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.(1+x)+(1+x)2+…+(1+x)n的所有二项式的各项系数和是( )
| A. | 2n+1 | B. | 2n+1+1 | C. | 2n+1-1 | D. | 2n+1-2 |
7.曲线C以双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}$=1的右焦点F为焦点,曲线C上的点到焦点F的距离与到直线x=-2的距离相等,则曲线C上的任意一点P到y轴的距离与到直线x-y+4=0的距离和的最小值为( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{2}$-1 | C. | 3$\sqrt{2}$+2 | D. | 3$\sqrt{2}$-2 |
4.已知函数y=-x2+3x,直线l1:x=t和l2:x=t+1(其中0≤t≤2,t为常数),若直线l1,l2,x轴与函数y=f(x)的图象所围成的封闭图形的面积为S,则S的最大值为( )
| A. | 2 | B. | $\frac{11}{6}$ | C. | $\frac{13}{6}$ | D. | 3 |
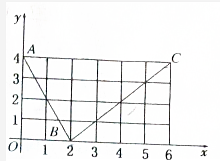 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).