题目内容
已知α∈（
，
），tan（α-7π）=-
，则sinα+cosα的值为
- A.±
- B.-
- C.
- D.-
B
分析：先根据诱导公式化简已知条件，求出正切值，然后根据正切值确定α∈（，π）的范围，在此范围中利用同角三角函数间的基本关系分别求出sinα和cosα即可求两者之和．
解答：tan（α-7π）=tan（-7π+α）=tanα=-，
∴α∈（，π），
根据cos2α=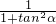
得到cosα=-
，
又由sin2α+cos2α=1，得到sinα=
∴sinα+cosα=-．
故选B
点评：本题重在考查学生对诱导公式及同角三角函数间的基本关系的运用，解此题时不要忽视由正切值确定α的范围．
分析：先根据诱导公式化简已知条件，求出正切值，然后根据正切值确定α∈（
，π）的范围，在此范围中利用同角三角函数间的基本关系分别求出sinα和cosα即可求两者之和．解答：tan（α-7π）=tan（-7π+α）=tanα=-
，∴α∈（
，π），根据cos2α=
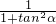得到cosα=-，又由sin2α+cos2α=1，得到sinα=
∴sinα+cosα=-
．故选B
点评：本题重在考查学生对诱导公式及同角三角函数间的基本关系的运用，解此题时不要忽视由正切值确定α的范围．
练习册系列答案
相关题目
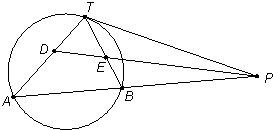如图，PT是⊙O的切线，切点为T，直线PA与⊙O交于A、B两点，∠TPA的平分线分别交直线TA、TB于D、E两点，已知PT=2，