题目内容

已知向量
a
，
b
，
c
满足
a
+
b
+
c
=0，|c|=2
3
，
c
与
a
-
b
所成的角为120°，则当t∈R时，|t
a
+（1-t）
b
|的取值范围是
[
3
2
，+∞)
[
3
2
，+∞)
．
分析：利用向量的线性运算、夹角的意义、共线定理并画出图形即可求出．
解答：解：由题意画出图形：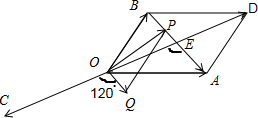
设
OA
=
a
，
OB
=
b
，
OD
=(
a
+
b
)=-
c
=-
OC
，
BA
=
a
-
b
．
∵|
c
|=2
3
，
c
与
a
-
b
所成的角为120°，
∴|
a
+
b
|=2
3
，∠OEA=120°．
设
OP
=t
a
+(1-t)
b
，即
OP
=t
OA
+(1-t)
OB
，
∴
BP
=t
BA
，
由图可知：当
OP
⊥
BA
时，|
OP
|取得最小值．
在Rt△OPE中，|
OP
|=|
OE
|sin60°=
1
2
×2
3
×
3
2
=
3
2
．
故当t∈R时，|t
a
+（1-t）
b
|的取值范围是[
3
2
，+∞)．
故答案为[
3
2
，+∞)．
点评：熟练掌握向量的线性运算、夹角的意义、共线定理是解题的关键．
练习册系列答案
相关题目
已知向量
α
=(
3
sinωx，cosωx），
β
=(cosωx，cosωx)，记函数f（x）=
α
•
β
，已知f（x）的周期为π．
（1）求正数ω之值；
（2）当x表示△ABC的内角B的度数，且△ABC三内角A、B、C满sin2B=sinA•sinC，试求f（x）的值域．
已知向量sinωx，cosωx），，记函数f（x）=，已知f（x）的周期为π．
（1）求正数ω之值；
（2）当x表示△ABC的内角B的度数，且△ABC三内角A、B、C满sin2B=sinAsinC，试求f（x）的值域．
已知向量sinωx，cosωx），，记函数f（x）=，已知f（x）的周期为π．
（1）求正数ω之值；
（2）当x表示△ABC的内角B的度数，且△ABC三内角A、B、C满sin2B=sinA•sinC，试求f（x）的值域．
已知向量sinωx，cosωx），，记函数f（x）=，已知f（x）的周期为π．
（1）求正数ω之值；
（2）当x表示△ABC的内角B的度数，且△ABC三内角A、B、C满sin2B=sinA•sinC，试求f（x）的值域．

已知向量, ,记函数已知的周期为π.

（1）求正数之值;

（2）当x表示△ABC的内角B的度数，且△ABC三内角A、B、C满sin,试求f(x)的值域.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网