题目内容
已知函数f(x)=log3(ax+b)的图象经过点A(2,1)、B(5,2),
(1)求函数f(x)的解析式及定义域;
(2)求f(14)÷f(
)的值.
(1)求函数f(x)的解析式及定义域;
(2)求f(14)÷f(
| ||
| 2 |
(1)因为函数f(x)=log3(ax+b)的图象经过点A(2,1)、B(5,2),
所以
,即
,
所以
,解得
.
所以f(x)=log3(2x-1),定义域为(
,+∞).
(2)f(14)÷f(
)=log327÷log3
=3÷
=6.
所以
|
|
所以
|
|
所以f(x)=log3(2x-1),定义域为(
| 1 |
| 2 |
(2)f(14)÷f(
| ||
| 2 |
| 3 |
| 1 |
| 2 |

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象大致是
的图象大致是


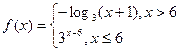 ,记
,记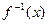 为
为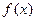 的反函数,且
的反函数,且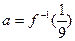 ,则
,则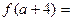 __________
__________ ,则
,则 等于( )
等于( )