题目内容
已知函数f(x)=
(x≠-
,a>0),且f(1)=log162,f(-2)=1.
(1)求函数f(x)的表达式;
(2)若数列xn的项满足xn=[1-f(1)]•[1-f(2)]•…•[1-f(n)],试求x1,x2,x3,x4;
(3)猜想数列xn的通项,并用数学归纳法证明.
| bx+1 |
| (ax+1)2 |
| 1 |
| a |
(1)求函数f(x)的表达式;
(2)若数列xn的项满足xn=[1-f(1)]•[1-f(2)]•…•[1-f(n)],试求x1,x2,x3,x4;
(3)猜想数列xn的通项,并用数学归纳法证明.
(1)∵f(x)=
(x≠-
,a>0),且f(1)=log162,f(-2)=1.
∴
=log162=
,
=1
解得:
∴函数f(x)=
(2)由(1)中f(x)=
∴xn=[1-f(1)]•[1-f(2)]•…•[1-f(n)],
当n=1时,x1=
.
当n=2时,x2=
,
当n=3时,x3=
,
当n=4时,x4=
(3)由(2)中结论我们易得:xn=
.
当n=1时,结论显然成立
设n=k时,结论成立,即xk=
则当n=k+1时,xk+1=xk•[1-
]=
•[1-
]=
即n=k+1时,结论也成立.
故xn=
.
| bx+1 |
| (ax+1)2 |
| 1 |
| a |
∴
| b+1 |
| (a+1)2 |
| 1 |
| 4 |
| -2b+1 |
| (-2a+1)2 |
解得:
|
∴函数f(x)=
| 1 |
| (x+1)2 |
(2)由(1)中f(x)=
| 1 |
| (x+1)2 |
∴xn=[1-f(1)]•[1-f(2)]•…•[1-f(n)],
当n=1时,x1=
| 3 |
| 4 |
当n=2时,x2=
| 4 |
| 6 |
当n=3时,x3=
| 5 |
| 8 |
当n=4时,x4=
| 6 |
| 10 |
(3)由(2)中结论我们易得:xn=
| n+2 |
| 2(n+1) |
当n=1时,结论显然成立
设n=k时,结论成立,即xk=
| k+2 |
| 2(k+1) |
则当n=k+1时,xk+1=xk•[1-
| 1 |
| (k+2)2 |
| k+2 |
| 2(k+1) |
| 1 |
| (k+2)2 |
| (k+2)+1 |
| 2[(k+1)+1] |
即n=k+1时,结论也成立.
故xn=
| n+2 |
| 2(n+1) |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
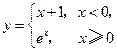 的反函数是__________.
的反函数是__________.



 中,若
中,若 ,
, (
( ),则
),则 .
.

 ,那么
,那么 的取值范围是( )
的取值范围是( )
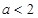 且
且

 或
或