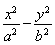题目内容
设f(x)是定义在R上的奇函数,且f(-1)=0,当x>0时,(x2+1)f′(x)-2xf(x)<0,则不等式f(x)>0的解集为________.
(-∞,-1)∪(0,1)
【解析】因为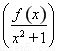 ′=
′= ,而(x2+1)f′(x)-2xf(x)<0,所以
,而(x2+1)f′(x)-2xf(x)<0,所以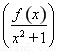 ′<0,令g(x)=
′<0,令g(x)=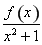 ,则函数g(x)在(0,+∞)单调递减,且也为奇函数,g(-1)=-g(1)=0,作出函数g(x)的大致示意图,由图可知g(x)>0的解集为(-∞,-1)∪(0,1),即为不等式f(x)>0的解集.
,则函数g(x)在(0,+∞)单调递减,且也为奇函数,g(-1)=-g(1)=0,作出函数g(x)的大致示意图,由图可知g(x)>0的解集为(-∞,-1)∪(0,1),即为不等式f(x)>0的解集.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目