题目内容
(本小题满分12分)已知二次函数f(x)满足条件: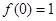 ,
,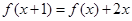
(1)求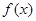
(2)讨论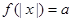
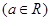 的解的个数
的解的个数
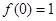 ,
,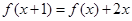
(1)求
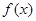
(2)讨论
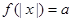
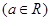 的解的个数
的解的个数(1) f(x)=x2-x+1
(2)

(3)1.当a<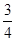 时,方程无解
时,方程无解
2.当a=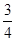 或a>1时,方程有两个解
或a>1时,方程有两个解
3.当a=1时方程有三个解
4.当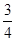 <a<1时,方程有四个解.
<a<1时,方程有四个解.
(2)

(3)1.当a<
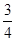 时,方程无解
时,方程无解2.当a=
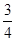 或a>1时,方程有两个解
或a>1时,方程有两个解3.当a=1时方程有三个解
4.当
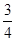 <a<1时,方程有四个解.
<a<1时,方程有四个解.(1)利用待定系数法因为f(0)=1,所以设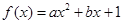 ,
,
根据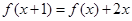 可得到一个关于x的恒等式,根据含x的各对应系数相等可得a,b的值.
可得到一个关于x的恒等式,根据含x的各对应系数相等可得a,b的值.
(2)在(1)的基础上,因为y=f(|x|)是偶函数,所以可先画出x>0时,y=f(|x|)的图像,再根据对称性画出y轴左侧的图像即可.然后再从图像可以确定当直线y=a与y=f(|x|)的图像交点情况不同时,对应的a的取值范围.
(1)求出f(x)给4分 f(x)=x2-x+1
(2)画出图像再给4分

(3)利用图像分类讨论再给4分
其它解法自已控制.
1.当a<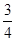 时,方程无解
时,方程无解
2.当a=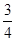 或a>1时,方程有两个解
或a>1时,方程有两个解
3.当a=1时方程有三个解
4.当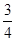 <a<1时,方程有四个解.
<a<1时,方程有四个解.
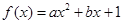 ,
,根据
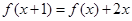 可得到一个关于x的恒等式,根据含x的各对应系数相等可得a,b的值.
可得到一个关于x的恒等式,根据含x的各对应系数相等可得a,b的值.(2)在(1)的基础上,因为y=f(|x|)是偶函数,所以可先画出x>0时,y=f(|x|)的图像,再根据对称性画出y轴左侧的图像即可.然后再从图像可以确定当直线y=a与y=f(|x|)的图像交点情况不同时,对应的a的取值范围.
(1)求出f(x)给4分 f(x)=x2-x+1
(2)画出图像再给4分

(3)利用图像分类讨论再给4分
其它解法自已控制.
1.当a<
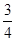 时,方程无解
时,方程无解2.当a=
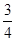 或a>1时,方程有两个解
或a>1时,方程有两个解3.当a=1时方程有三个解
4.当
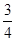 <a<1时,方程有四个解.
<a<1时,方程有四个解.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
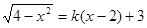 有两个不等实根,则k的取值范围是( )
有两个不等实根,则k的取值范围是( )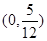
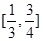
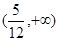
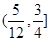
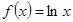 在点
在点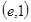 处的为_______________________________.
处的为_______________________________.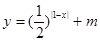 的图象与
的图象与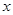 轴有公共点,则
轴有公共点,则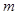 的取值范围是( )
的取值范围是( )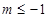
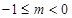
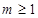
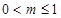
 的函数
的函数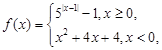 若关于x的方程
若关于x的方程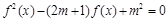 有5个不同的实数解,则
有5个不同的实数解,则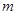 =( )
=( )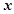 的方程
的方程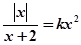 有四个不同的实数解,则实数
有四个不同的实数解,则实数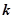 的取值范围为( )
的取值范围为( ) ,1)
,1)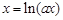 (
( 为常数,
为常数, ),则下列判断正确的是( ).
),则下列判断正确的是( ).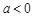 时,没有实根
时,没有实根 时,有一个实根
时,有一个实根 时,有三个实根
时,有三个实根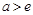 时,有两个实根
时,有两个实根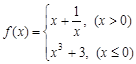 ,则函数
,则函数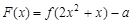 (
(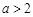 )的零点个数不可能为 ( )
)的零点个数不可能为 ( )