题目内容
设定义域为 的函数
的函数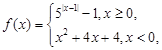 若关于x的方程
若关于x的方程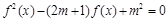 有5个不同的实数解,则
有5个不同的实数解,则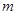 =( )
=( )
 的函数
的函数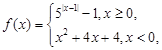 若关于x的方程
若关于x的方程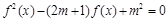 有5个不同的实数解,则
有5个不同的实数解,则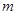 =( )
=( )| A.6 | B.4或6 | C.6或2 | D.2 |
A
解:∵题中原方程f2(x)-(2m+1)f(x)+m2=0有5个不同的实数根,
∴即要求对应于f(x)等于某个常数有2个不同实数解,
∴故先根据题意作出f(x)的简图:
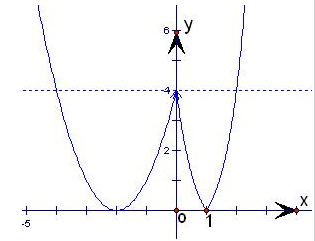
由图可知,只有当f(x)=4时,它有三个根.
故关于x的方程f2(x)-(2m+1)f(x)+m2=0有一个实数根4.
∴42-4(2m+1)+m2=0,
∴m=6
故答案为A
∴即要求对应于f(x)等于某个常数有2个不同实数解,
∴故先根据题意作出f(x)的简图:

由图可知,只有当f(x)=4时,它有三个根.
故关于x的方程f2(x)-(2m+1)f(x)+m2=0有一个实数根4.
∴42-4(2m+1)+m2=0,
∴m=6
故答案为A

练习册系列答案
相关题目
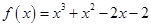 的一个正实数零点,其参考数据如下:
的一个正实数零点,其参考数据如下: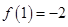


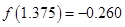

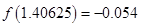
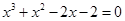 的一个近似根(精确到0.1)为 ( )
的一个近似根(精确到0.1)为 ( ) 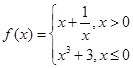 ,则方程
,则方程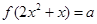 (
(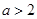 )的根的个数不可能为( )
)的根的个数不可能为( ) 的图像与
的图像与 轴没有公共点,则m的取值范围是__________(用区间表示)。
轴没有公共点,则m的取值范围是__________(用区间表示)。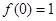 ,
,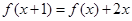
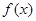
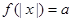
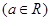 的解的个数
的解的个数 的零点为
的零点为 ,函数
,函数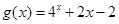 的零点为
的零点为 ,若
,若
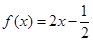


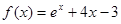 的零点所在的区间为
的零点所在的区间为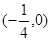
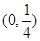
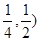
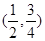
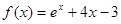 的零点所在的区间为( )
的零点所在的区间为( )


