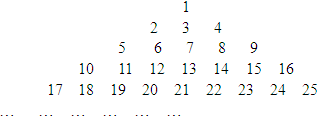题目内容
用三段论证明:直角三角形两锐角之和为 .
.
 .
.见解析
试题分析:证明:因为任意三角形三内角之和是
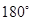 , 大前提
, 大前提而直角三角形是三角形, 小前提
所以直角三角形三内角之和为
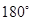 . 结论
. 结论设直角三角形两个锐角分别为
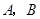 ,则有:
,则有: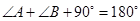 .
.因为等量减等量差相等, 大前提
所以
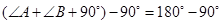 , 小前提
, 小前提所以
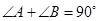 . 结论
. 结论点评:“三段论”是演绎推理的一般形式,包括:大前提——已知的一般原理;小前提,所研究的特殊情况;结论——根据一般原理,对特殊情况做出的判断。

练习册系列答案
相关题目
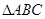 的三边长为
的三边长为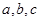 ,内切圆半径为
,内切圆半径为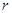 (用
(用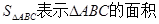 ),则
),则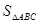
 ;类比这一结论有:若三棱锥
;类比这一结论有:若三棱锥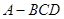 的内切球半径为
的内切球半径为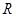 ,则三棱锥体积
,则三棱锥体积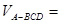
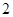 的自然数
的自然数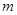 的
的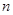 次方幂有如下分解方式:
次方幂有如下分解方式: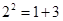
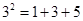
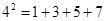
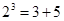
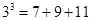
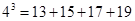
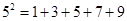 , 若
, 若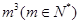 的分解中最小的数是73,则
的分解中最小的数是73,则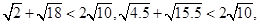
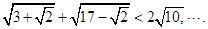 根据以上规律,试写出一个对正整数
根据以上规律,试写出一个对正整数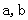 成立的条件不等式 。
成立的条件不等式 。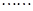
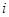 行里的最后一个数字是多少?
行里的最后一个数字是多少?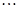 这些数叫做三角形,这是因为这些数目的点可以排成一个正三角形(如下面),则第七个三角形数是 .
这些数叫做三角形,这是因为这些数目的点可以排成一个正三角形(如下面),则第七个三角形数是 .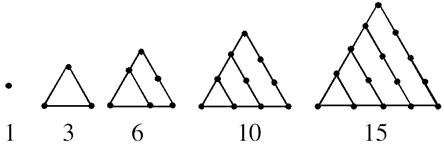
 行最右边的数是
行最右边的数是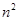 , 那么第20行最左边的数是_____________.
, 那么第20行最左边的数是_____________.