题目内容
（2013•临沂二模）设第一象限内的点（x，y）满足
，若目标函数z=ax+by（a＞0，b＞0）的最大值是4，则
+
的最小值为（ ）
|
| 1 |
| a |
| 1 |
| b |
分析：由线性约束条件求出最优解，代入线性目标函数得到a+b=1，然后利用
+
等于(
+
)(a+b)展开整理，最后利用基本不等式求最小值．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
解答：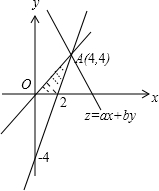
解：因为点（x，y）是第一象限内的点，结合约束条件
得可行域如图，
所以最优解为A（4，4），即4a+4b=4，所以a+b=1．
则
+
=(a+b)(
+
)=
+
+2
≥2
+2=4．
当且仅当
=
，即a=b是取“=”．
所以
+
的最小值为4．
故选B．
解：因为点（x，y）是第一象限内的点，结合约束条件
|
所以最优解为A（4，4），即4a+4b=4，所以a+b=1．
则
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| a |
| b |
| b |
| a |
≥2
|
当且仅当
| a |
| b |
| b |
| a |
所以
| 1 |
| a |
| 1 |
| b |
故选B．
点评：本题考查了简单的线性规划，考查了利用基本不等式求最值，解答此题的关键是对“1”的灵活运用，是基础题．
练习册系列答案
同步练习河南大学出版社系列答案
相关题目