题目内容

（本小题共13分）

某同学设计一个摸奖游戏：箱内有红球3个，白球4个，黑球5个．每次任取一个，有放回地抽取3次为一次摸奖．至少有两个红球为一等奖，记2分；红、白、黑球各一个为二等奖，记1分；否则没有奖，记0分．

（I）求一次摸奖中一等奖的概率；

（II）求一次摸奖得分的分布列和期望．

 

【答案】

 

【解析】解：（I）每次有放回地抽取，取到红球的概率为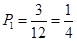；取到白球的概率为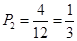；取到

        黑球的概率为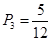； -------------3分

一次摸奖中一等奖的概率为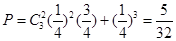．     ---------5分

   （II）设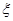表示一次摸奖的得分，则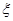可能的取值为0，1，2． -----------6分

；

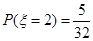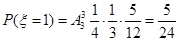； ---------8分

   ---10分

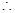一次摸奖得分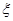的分布列为

2

1

0

P

期望为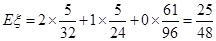． -------------------13分

 

练习册系列答案
相关题目

（本小题共13分）

已知函数

   （I）若x=1为的极值点，求a的值；

   （II）若的图象在点（1，）处的切线方程为，

（i）求在区间[-2，4]上的最大值；

（ii）求函数的单调区间.


（本小题共13分）
已知函数．
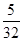
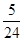
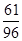
（Ⅰ）若在处取得极值，求a的值；
（Ⅱ）求函数在上的最大值．

（本小题共13分）

已知向量，设函数.

（Ⅰ）求函数在上的单调递增区间；

（Ⅱ）在中，，，分别是角，，的对边，为锐角，若，，的面积为，求边的长．

 

（本小题共13分）

某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖．

（Ⅰ）求分别获得一、二、三等奖的概率；

（Ⅱ）设摸球次数为，求的分布列和数学期望．

 

（本小题共13分）
已知函数
（I）当a=1时，求函数的最小正周期及图象的对称轴方程式；
（II）当a=2时，在的条件下，求的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网