题目内容
【题目】已知四棱锥
的底面为平行四边形，
，
为
中点．
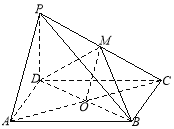
（1）求证:
．
（2）若
，求证:
．
【答案】（1）详见解析（2）详见解析
【解析】
试题分析：（1）设AC∩BD=H，连接EH，由平行四边形的性质结合题意证出MH为△PAC中位线，从而得到MH∥PA，利用线面平行的判定定理，即可证出PA∥平面MBD．（2）由线面垂直的定义证出PD⊥AD，结合AD⊥PB得到AD⊥平面PDB，得AD⊥BD，再根据PD⊥BD且PD、AD是平面PAD内的相交直线，可得BD⊥平面PAD
试题解析：（1）因为底面
是平行四边形，所以点
为
的中点， 1分
又
为
的中点，所以
3分
因为
，
，所以
．5分
（2）因为
平面，
，所以
6分
因为
，
，
，
，
所以
平面
8分
因为
，所以
9分
因为平面，
，所以 
10分
又因为，
，
，
，
所以
平面
．12分
练习册系列答案
相关题目
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，算得，χ2≈7.8.附表：
P(χ2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是( )
A. 有99.9%以上的把握认为“爱好该项运动与性别有关”
B. 有99.9%以上的把握认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动和性别有关”
D. 有99%以上的把握认为“爱好该项运动和性别无关”
