题目内容
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题,每人答对其中
题,每人答对其中 题就停止答题,即闯关成功.已知在
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题的概率都是
道题,乙答对每道题的概率都是 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
解:(Ⅰ)设甲、乙闯关成功分别为事件 ,则
,则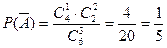 ,………………………………………………………2分
,………………………………………………………2分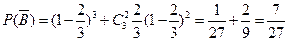 , ………………………………4分
, ………………………………4分
所以,甲、乙至少有一人闯关成功的概率是: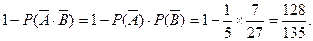 ………………………………6分
………………………………6分
(Ⅱ)由题意,知ξ的可能取值是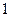 、
、 .
.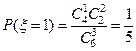 ,
,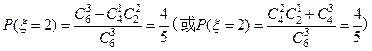
则 的分布列为
的分布列为
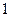

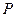
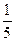
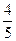
……10分
∴ 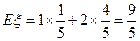 .………………………………………………………12分
.………………………………………………………12分
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
[2014·北京模拟]如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂1种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有( )
| A.72种 | B.96种 | C.108种 | D.120种 |
阅读右面的程序框图,运行相应的程序,输出的结果为( )
A.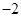 | B. | C. | D. |
 ,求
,求 ,若连续射击6次,且各次射击是否命中目标相互之间没有影响.
,若连续射击6次,且各次射击是否命中目标相互之间没有影响. ,构造数列
,构造数列 ,使
,使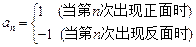 ,记
,记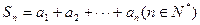 .
.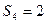 的概率;
的概率;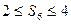 的概率.
的概率. ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.