题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求椭圆C的方程;
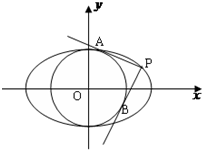
(2)椭圆C上是否存在点P,使得过点P引圆O:x2+y2=b2的两条切线PA、PB互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)直接根据条件列出
,解方程求出b,c即可得到椭圆C的方程;
(2)先根据条件分析出AOBP为正方形,|AO|=|AP|,得到关于点P坐标的等式;再结合点P在椭圆上即可求出点P的坐标.
|
(2)先根据条件分析出AOBP为正方形,|AO|=|AP|,得到关于点P坐标的等式;再结合点P在椭圆上即可求出点P的坐标.
解答:解:(1)设椭圆的半焦距为c,依题意
…(3分)
∴b=2,…(4分)
∴所求椭圆方程为
+
=1. (5分)
(2)设P点坐标为(x0,y0),
依题意,∠APO=∠BPO=90°,又∠APB=90°.所以AOBP为矩形,
又|BP|=|AP|,|BO|=|AO|.所以AOBP为正方形,则有|AO|=|AP|.(7分)
即|OA|=
有2=
两边平方得x02+y02=8…①(9分)
又因为P(x0,y0)在椭圆上,所以4x02+9y02=36…②
①,②联立解得x02=
,y02=
(11分)
所以满足条件的有以下四组解
,
,
,
.
所以,椭圆C上存在四个点(
,
),(
,-
),(-
,
),(-
,-
),
分别由这四个点向圆O所引的两条切线均互相垂直.(14分)
|
∴b=2,…(4分)
∴所求椭圆方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)设P点坐标为(x0,y0),
依题意,∠APO=∠BPO=90°,又∠APB=90°.所以AOBP为矩形,
又|BP|=|AP|,|BO|=|AO|.所以AOBP为正方形,则有|AO|=|AP|.(7分)
即|OA|=
| |OP|2-|AP|2 |
| x02+y02-4 |
两边平方得x02+y02=8…①(9分)
又因为P(x0,y0)在椭圆上,所以4x02+9y02=36…②
①,②联立解得x02=
| 36 |
| 5 |
| 4 |
| 5 |
所以满足条件的有以下四组解
|
|
|
|
所以,椭圆C上存在四个点(
6
| ||
| 5 |
2
| ||
| 5 |
6
| ||
| 5 |
2
| ||
| 5 |
6
| ||
| 5 |
2
| ||
| 5 |
6
| ||
| 5 |
2
| ||
| 5 |
分别由这四个点向圆O所引的两条切线均互相垂直.(14分)
点评:本题主要考查圆与圆锥曲线的综合问题.解决第二问的关键在于根据条件分析出AOBP为正方形,|AO|=|AP|,得到关于点P坐标的等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目