Question

【题目】设函数f（x）在定义域[﹣1，1]是奇函数，当x∈[﹣1，0]时，f（x）=﹣3x2 ．
（1）当x∈[0，1]，求f（x）；
（2）对任意a∈[﹣1，1]，x∈[﹣1，1]，不等式f（x）≤2cos2θ﹣asinθ+1都成立，求θ的取值范围．

Answer 1

【答案】
（1）解：由题意可知，f（﹣x）=﹣f（x），

设x∈[0，1]，则﹣x∈[﹣1，0]，

则f（﹣x）=﹣3x2，

∴f（﹣x）=﹣3x2=﹣f（x），

即f（x）=3x2

（2）解：由（1）知f（x）= ，

∵不等式f（x）≤2cos2θ﹣asinθ+1都成立，

∴f（x）max≤2cos2θ﹣asinθ+1都成立，

∵f（x）max=f（1）=3，

∴2cos2θ﹣asinθ+1≥3，

即2sin2θ+asinθ≤0，

设f（a）=2sin2θ+asinθ，

∵a∈[﹣1，1]，

∴ ，即 ，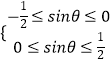

∴sinθ=0，

即θ=kπ，k∈Z

【解析】（1）根据函数奇偶性的性质，即可求出当x∈[0，1]，f（x）的表达式；（2）将不等式恒成立，转换为最值恒成立即可得到结论．