题目内容
【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:Sn2=3n2an+Sn﹣12 , an≠0,n≥2,n∈N* .
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
【答案】
(1)解:在 ![]() =3n2an+
=3n2an+ ![]() 中分别令n=2,n=3,及a1=a
中分别令n=2,n=3,及a1=a
得(a+a2)2=12a2+a2,(a+a2+a3)2=27a3+(a+a2)2,
因为an≠0,所以a2=12﹣2a,a3=3+2a.
因为数列{an}是等差数列,所以a1+a3=2a2,
即2(12﹣2a)=a+3+2a,解得a=3.)
经检验a=3时,an=3n,Sn= ![]() ,Sn﹣1=
,Sn﹣1= ![]()
满足 ![]() =3n2an+
=3n2an+ ![]() .
.
(2)解:由 ![]() =3n2an+
=3n2an+ ![]() ,得
,得 ![]() ﹣
﹣ ![]() =3n2an,
=3n2an,
即(Sn+Sn﹣1)(Sn﹣Sn﹣1)=3n2an,
即(Sn+Sn﹣1)an=3n2an,因为an≠0,
所以Sn+Sn﹣1=3n2,(n≥2),①
所以Sn+1+Sn=3(n+1)2,②
②﹣①,得an+1+an=6n+3,(n≥2).③
所以an+2+an+1=6n+9,④
④﹣③,得an+2﹣an=6,(n≥2)
即数列a2,a4,a6,…,及数列a3,a5,a7,…都是公差为6的等差数列,
因为a2=12﹣2a,a3=3+2a.
∴an= 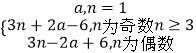
要使数列{an}是递增数列,须有a1<a2,且当n为大于或等于3的奇数时,an<an+1,
且当n为偶数时,an<an+1,即a<12﹣2a,
3n+2a﹣6<3(n+1)﹣2a+6(n为大于或等于3的奇数),
3n﹣2a+6<3(n+1)+2a﹣6(n为偶数),
解得 ![]() <a<
<a< ![]() .
.
所以M=( ![]() ,
, ![]() ),当a∈M时,数列{an}是递增数列
),当a∈M时,数列{an}是递增数列
【解析】(1)分别令n=2,n=3,及a1=a,结合已知可由a表示a2 , a3 , 结合等差数列的性质可求a,(2)由 ![]() =3n2an+
=3n2an+ ![]() ,得
,得 ![]() ﹣
﹣ ![]() =3n2an , 两式相减整理可得所以Sn+Sn﹣1=3n2 , 进而有Sn+1+Sn=3(n+1)2 , 两式相减可得数列的偶数项和奇数项分别成等差数列,结合数列的单调性可求a
=3n2an , 两式相减整理可得所以Sn+Sn﹣1=3n2 , 进而有Sn+1+Sn=3(n+1)2 , 两式相减可得数列的偶数项和奇数项分别成等差数列,结合数列的单调性可求a
【考点精析】通过灵活运用等差关系的确定,掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列即可以解答此题.
)那么这个数列就叫做等差数列即可以解答此题.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案