题目内容
如图所示，AB、CD都是圆的弦，且AB∥CD，F为圆上一点，延长FD、AB交于点E.
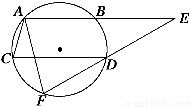
求证：AE·AC＝AF·DE.
见解析
【解析】
证明 连接BD，因为AB∥CD，所以BD＝AC.
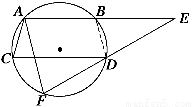
因为A、B、D、F四点共圆，所以∠EBD＝∠F.
因为∠E为△EBD和△EFA的公共角，
所以△EBD∽△EFA.
所以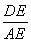
＝
.
所以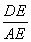
＝
，
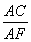即AE·AC＝AF·DE.
练习册系列答案
相关题目
题目内容
如图所示，AB、CD都是圆的弦，且AB∥CD，F为圆上一点，延长FD、AB交于点E.
求证：AE·AC＝AF·DE.
见解析
【解析】
证明 连接BD，因为AB∥CD，所以BD＝AC.
因为A、B、D、F四点共圆，所以∠EBD＝∠F.
因为∠E为△EBD和△EFA的公共角，
所以△EBD∽△EFA.
所以＝.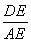
所以＝，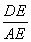
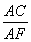即AE·AC＝AF·DE.
