Question

已知直线l₁:y=x与直线l₂:y=-x,在两直线的上方有一点P,P到直线l₁、l₂的距离分别为与,再过点P分别作l₁、l₂的垂线,垂足分别为A、B.求:

(1)P点坐标;

(2)|AB|的值.

Answer 1

思路解析：本题考查点到直线的距离,可以把点P的坐标直接设出,代入距离公式,再根据实际图形即可求出相应元素.

解：(1)设P(x,y),则由点到直线的距离公式得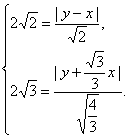

因为P在两直线的上方,所以y-x＞0,y+x＞0.

解上述方程组可得x=0,y=4.

满足x＜y,y＞0,故所求点P坐标为(0,4).

(2)由已知点A、P、B、O四点共圆,圆的直径2R=|OP|=4,

在△ABC中,由正弦定理可得

|AB|=4·sin75°=.