题目内容
若函数f（x）=x3+3bx-3b在区间（0，1）内存在极小值，则实数b的取值范围为
- A.-1＜b＜0
- B.b＞-1
- C.b＜0
- D.
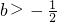
A
分析：求出函数的导数，然后令导数为零，求出函数的极值，最后确定b的范围．
解答：由题意得f′（x）=3x2-3b，
令f′（x）=0，则x=±
又∵函数f（x）=x3-3bx+b在区间（0，1）内有极小值，
∴0＜＜1，
∴b∈（0，1），
故选A．
点评：熟练运用函数的导数求解函数的极值问题，同时考查了分析问题的能力，属于基础题．
分析：求出函数的导数，然后令导数为零，求出函数的极值，最后确定b的范围．
解答：由题意得f′（x）=3x2-3b，
令f′（x）=0，则x=±
又∵函数f（x）=x3-3bx+b在区间（0，1）内有极小值，
∴0＜
＜1，∴b∈（0，1），
故选A．
点评：熟练运用函数的导数求解函数的极值问题，同时考查了分析问题的能力，属于基础题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目