题目内容
已知函数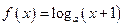 ,
,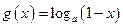 ,
,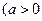 ,且
,且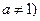 .
.
(1) 求函数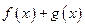 的定义域;
的定义域;
(2) 判断函数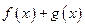 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3) 求使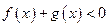 成立的
成立的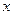 的集合.
的集合.
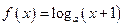 ,
,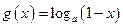 ,
,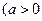 ,且
,且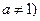 .
.(1) 求函数
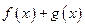 的定义域;
的定义域;(2) 判断函数
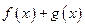 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3) 求使
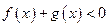 成立的
成立的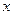 的集合.
的集合.(1)函数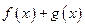 的定义域为
的定义域为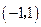 .
.
(2)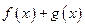 是
是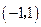 上的偶函数.
上的偶函数.
(3)当 时,
时,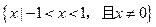 .当
.当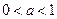 时,
时,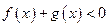 成立的
成立的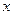 的集合是
的集合是 .
.
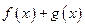 的定义域为
的定义域为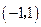 .
.(2)
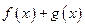 是
是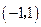 上的偶函数.
上的偶函数.(3)当
 时,
时,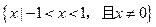 .当
.当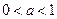 时,
时,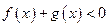 成立的
成立的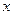 的集合是
的集合是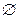 .
.(1)由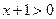 ,
,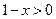 得
得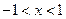 ,所以,函数
,所以,函数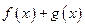 的定义域为
的定义域为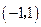 .
.
(2)对任意的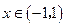 ,
,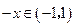 有
有
 .
.
所以,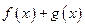 是
是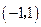 上的偶函数.
上的偶函数.
(3)当 时,要使
时,要使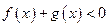 成立,
成立,
则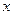 应满足
应满足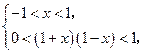
解得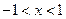 ,且
,且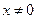 .
.
所以,当 时,使
时,使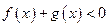 成立的
成立的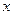 的集合是
的集合是
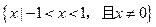 .
.
当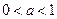 时,要使
时,要使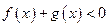 成立,则
成立,则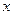 应满足
应满足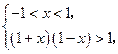
满足条件的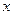 不存在.
不存在.
所以,当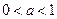 时,
时,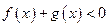 成立的
成立的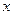 的集合是
的集合是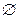 .
.
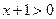 ,
,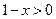 得
得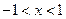 ,所以,函数
,所以,函数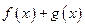 的定义域为
的定义域为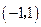 .
.(2)对任意的
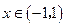 ,
,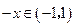 有
有 .
.所以,
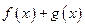 是
是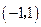 上的偶函数.
上的偶函数.(3)当
 时,要使
时,要使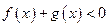 成立,
成立,则
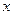 应满足
应满足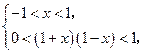
解得
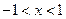 ,且
,且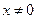 .
.所以,当
 时,使
时,使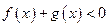 成立的
成立的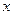 的集合是
的集合是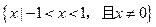 .
.当
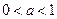 时,要使
时,要使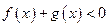 成立,则
成立,则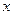 应满足
应满足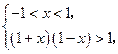
满足条件的
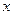 不存在.
不存在.所以,当
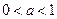 时,
时,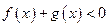 成立的
成立的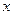 的集合是
的集合是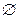 .
.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 +
+

 ,
, ,试比较
,试比较 和
和 的大小.
的大小.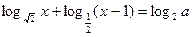 有解,则实数a的取值范围是
有解,则实数a的取值范围是  ,等差数列
,等差数列 的公差为
的公差为 .若
.若 ,则
,则 .
. ,则
,则 的大小关系是( )
的大小关系是( )


