Question

下列命题中，正确的是

1. A.
   数列{a_n}一定是等比数列
2. B.
   若a、b、c是实数，且b²=ac，则a、b、c一定成等比数列
3. C.
   若数列{a_n}相邻两项满足a_n=qa_n-1（q是常数），则{a_n}一定成等比数列
4. D.
   若a、b、c是实数且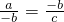，则-a、b、-c成等比数列

Answer 1

D
分析：A中，各项不清楚，各项的关系更未知，不成立；B中，a、b、c为0时，不成立；C中，q为0时，不成立；D，根据等比数列的定义，可判断．
解答：对于A，因为各项不清楚，各项的关系更未知，故不成立；
对于B，a、b、c为0时，满足a、b、c是实数，且b²=ac，但a、b、c不成等比数列；
对于C，q为0时，不成立
对于D，根据等比数列的定义，可知结论成立
故选D．
点评：本题的考点是等比关系的确定，主要考查等比数列的定义，应注意等比数列的各项不为0，公比不为0．