题目内容
下列命题中，正确的是
①平面向量
与
的夹角为60°，
=（2，0），|
|=1，则|
+
|=
；
②已知
=（sinθ，
），
=（1，
）其中θ∈（π，
）则
⊥
；
③O是△ABC所在平面上一定点，动点P满足：
=
+λ（
+
），λ∈（0，+∞），则直线AP一定通过△ABC的内心．
①②③
①②③
①平面向量
| a |
| b |
| a |
| b |
| a |
| b |
| 7 |
②已知
| a |
| 1+cosθ |
| b |
| 1-cosθ |
| 3π |
| 2 |
| a |
| b |
③O是△ABC所在平面上一定点，动点P满足：
| OP |
| OA |
| ||
| sinC |
| ||
| sinB |
分析：①由
=(2，0)，求出|
|，在三个向量
，
，
+
构成的三角形中，运用余弦定理求|
+
|；
②写出两个向量的数量积，运用同角三角函数的基本关系式整理即可得到结论；
③把给出等式中的角的正弦值用对应边长和外接圆半径表示，移向整理后得即
=2Rλ(
+
)．
由此式可知直线AP一定通过△ABC的内心．
| a |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
②写出两个向量的数量积，运用同角三角函数的基本关系式整理即可得到结论；
③把给出等式中的角的正弦值用对应边长和外接圆半径表示，移向整理后得即
| AP |
| ||
|
|
| ||
|
|
由此式可知直线AP一定通过△ABC的内心．
解答：解：①如图，
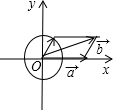
因为
=（2，0），所以|
|=
=2，
+
对应的向量是以
和
为邻边的平行四边形的对角线，
由余弦定理得：|
+
|=
=
=
，
所以①正确；
②由
=（sinθ，
），
=（1，
），
则
•
=sinθ+
=sinθ+
=sinθ+
=sinθ+|sinθ|，
因为θ∈（π，
），所以sinθ＜0，
所以
•
=sinθ-sinθ=0，所以
⊥
，
所以②正确；
③如图，
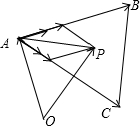
在△ABC中，由
=
=2R（R为三角形ABC外接圆半径），所以sinC=
，sinB=
，
所以
=
+λ（
+
）=
+λ(
+
)=
+2Rλ(
+
)，
即
=2Rλ(
+
)．
所以直线AP一定通过△ABC的内心．
所以③正确．
故答案为①②③
因为
| a |
| a |
| 22+02 |
| a |
| b |
| a |
| b |
由余弦定理得：|
| a |
| b |
|
|
22+12-2×2×1×(-
|
| 7 |
所以①正确；
②由
| a |
| 1+cosθ |
| b |
| 1-cosθ |
则
| a |
| b |
| (1+cosθ)(1-cosθ) |
| 1-cos2θ |
| sin2θ |
因为θ∈（π，
| 3π |
| 2 |
所以
| a |
| b |
| a |
| b |
所以②正确；
③如图，
在△ABC中，由
|
| ||
| sinC |
|
| ||
| sinB |
|
| ||
| 2R |
|
| ||
| 2R |
所以
| OP |
| OA |
| ||
| sinC |
| ||
| sinB |
| OA |
2R
| ||
|
|
2R
| ||
|
|
| OA |
| ||
|
|
| ||
|
|
即
| AP |
| ||
|
|
| ||
|
|
所以直线AP一定通过△ABC的内心．
所以③正确．
故答案为①②③
点评：本题考查了命题的真假的判断与运用，解答此题的关键是判断③，需要掌握的是
表示
方向上的单位向量，此题是中档题．
| ||
|
|
| a |
练习册系列答案
相关题目