题目内容
15.已知tan(α+β)=1,tan(α-β)=2,则$\frac{sin2α}{cos2β}$的值为1.分析 利用已知条件求出αβ的正切函数值,然后求解$\frac{sin2α}{cos2β}$的值.
解答 解:tan(α+β)=1,tan(α-β)=2,
$\frac{sin2α}{cos2β}$=$\frac{sin[(α+β)+(α-β)]}{cos[(α+β)-(α-β)]}$=$\frac{sin(α+β)cos(α-β)+cos(α+β)sin(α-β)}{cos(α+β)cos(α-β)+sin(α+β)sin(α-β)}$,
分式同除以cos(α+β)cos(α-β)),
$\frac{tan(α+β)+tan(α-β)}{1+tan(α+β)tan(α-β)}$=$\frac{1+2}{1+1×2}$=1.
故答案为:1.
点评 本题考查同角三角函数的基本关系式的化简求值,注意角的变换,考查计算能力.

练习册系列答案
相关题目
3.设x,y满足约束条件$\left\{\begin{array}{l}{x-2y≥-2}\\{3x-2y≤3}\\{x+y≥1}\end{array}\right.$,若x2+4y2≥m恒成立,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
5.某程序框图如图所示,若输出的S=41,则判断框内应填( )


| A. | k>4? | B. | k>5? | C. | k>6? | D. | k>7? |
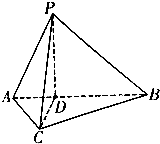 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.