题目内容
已知正三棱锥P-ABC中，底面边长为| 3 |
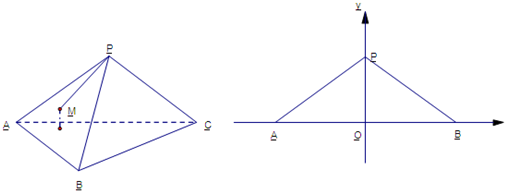
分析：由题意推出三角形的中心到四个顶点的距离相等，说明中心就是外接球的球心，求出球的半径，即可求出外接球的表面积．
解答：解：∵正三棱锥P-ABC中，底面边长为
，高为1，
得到△ABC的中心O到四个顶点的距离相等，
∴正三棱锥P-ABC的外接球的球心为O，外接球的半径为1，表面积为：4π．
故答案为：4π
| 3 |
得到△ABC的中心O到四个顶点的距离相等，
∴正三棱锥P-ABC的外接球的球心为O，外接球的半径为1，表面积为：4π．
故答案为：4π
点评：本题是基础题，考查空间想象能力，计算能力；正三角形的中心就是外接球的球心，是本题解题的关键，仔细观察和分析题意，是解好数学题目的前提．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
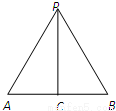
已知正三棱锥P-ABC主视图如图所示，其中△PAB中，AB=PC=2cm，则这个正三棱锥的左视图的面积为
