题目内容
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
【答案】
解:(1)要想使取出的3个球颜色全不相同,则乙必须取出黄球,甲取出的两个球为一个红球一个白球,乙取出黄球的概率是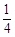 ,甲取出的两个球为一个红球一个白球的概率是
,甲取出的两个球为一个红球一个白球的概率是
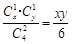 ,所以取出的3个球颜色全不相同的概率是
,所以取出的3个球颜色全不相同的概率是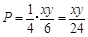 ,即甲获胜的概率为
,即甲获胜的概率为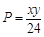 ,由
,由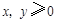 ,且
,且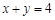 ,所以
,所以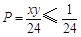
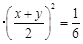 ,当
,当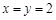 时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大.
时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大.
(2)设取出的3个球中红球的个数为ξ,则ξ的取值为0,1,2,3.
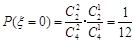 ,
,
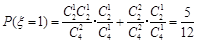 ,
,
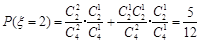 ,
,
 ,
,
所以取出的3个球中红球个数的期望: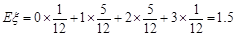 .
.
【解析】略

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目