题目内容
【题目】给出下列五个命题: ①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
【答案】①②
【解析】解:当x= ![]() 时,sin(2x﹣
时,sin(2x﹣ ![]() )=sin
)=sin ![]() =1,∴①正确; 当x=
=1,∴①正确; 当x= ![]() 时,tanx无意义,∴②正确;
时,tanx无意义,∴②正确;
当x>0时,y=sinx的图象为“波浪形“曲线,故③错误;
若 ![]() ,则2x1﹣
,则2x1﹣ ![]() =2x2﹣
=2x2﹣ ![]() +2kπ或2x1﹣
+2kπ或2x1﹣ ![]() +(2x2﹣
+(2x2﹣ ![]() )=2(
)=2( ![]() )=π+2kπ,
)=π+2kπ,
∴x1﹣x2=kπ或x1+x2= ![]() +kπ,k∈Z.故④错误.
+kπ,k∈Z.故④错误.
作出f(x)=sinx+2|sinx|在[0,2π]上的函数图象,如图所示:
则f(x)在[0,π]上过原点得切线为y=3x,设f(x)在[π,2π]上过原点得切线为y=k1x,
有图象可知当k1<k<3时,直线y=kx与f(x)有2个不同交点,
∵y=sinx在[0,π]上过原点得切线为y=x,∴k1<1,故⑤不正确.
故答案为:①②.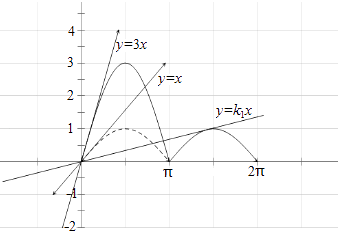
①计算2sin(2× ![]() ﹣
﹣ ![]() )是否为最值±2进行判断;②根据正切函数的性质判断;③根据正弦函数的图象判断;④由
)是否为最值±2进行判断;②根据正切函数的性质判断;③根据正弦函数的图象判断;④由 ![]() 得2x1﹣
得2x1﹣ ![]() 和2x2﹣
和2x2﹣ ![]() 关于对称轴对称或相差周期的整数倍;⑤作出函数图象,借助图象判断.
关于对称轴对称或相差周期的整数倍;⑤作出函数图象,借助图象判断.

 阅读快车系列答案
阅读快车系列答案【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高二年级有男生500人,女生400人,为了了解性别对维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频率统计表如表: 表一:男生测评结果统计
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | x | 5 |
表二:女生测评结果统计
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 | y |
参考数据:
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d).
,其中n=a+b+c+d).
(1)计算x,y的值;
(2)由表一表二中统计数据完成2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |