题目内容
已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,点M(m,0)到直线AP的距离为1.
(1)若直线AP的斜率为k,且|k|∈[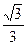 ,
,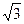 ],求实数m的取值范围;
],求实数m的取值范围;
(2)当m=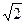 +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.
(1)若直线AP的斜率为k,且|k|∈[
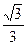 ,
,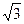 ],求实数m的取值范围;
],求实数m的取值范围;(2)当m=
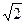 +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.1、m的取值范围是[-1,1-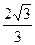 ]∪[1+
]∪[1+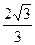 ,3].
,3].
2、x2-(2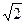 -1)y2=1.
-1)y2=1.
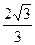 ]∪[1+
]∪[1+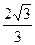 ,3].
,3].2、x2-(2
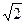 -1)y2=1.
-1)y2=1.(1)由条件得直线AP的方程y=k(x-1),即kx-y-k=0,
因为点M到直线AP的距离为1,
∴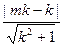 =1,即|m-1|=
=1,即|m-1|=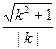 =
=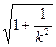 .
.
∵|k|∈[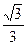 ,
,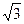 ],
],
∴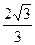 ≤|m-1|≤2.
≤|m-1|≤2.
解得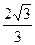 +1≤m≤3或-1≤m≤1-
+1≤m≤3或-1≤m≤1-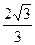 .
.
∴m的取值范围是[-1,1-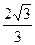 ]∪[1+
]∪[1+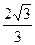 ,3].
,3].
(2)可设双曲线方程为x2-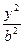 =1(b≠0),
=1(b≠0),
由M(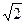 +1,0),A(1,0)得|AM|=
+1,0),A(1,0)得|AM|=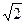 .
.
又因为M是△APQ的内心,M到AP的距离为1,
所以∠MAP=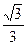 45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1.
45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1.
因此kAP=1,kAQ=-1(不妨设P在第一象限),直线PQ的方程为x=2+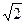 ,
,
直线AP的方程为y=x-1.
∴解得P的坐标是(2+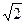 ,1+
,1+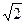 ).
).
将P点坐标代入x2-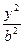 =1得b2=
=1得b2=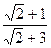 ,
,
所以所求双曲线方程为x2-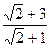 y2=1,
y2=1,
即x2-(2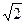 -1)y2=1.
-1)y2=1.
因为点M到直线AP的距离为1,
∴
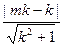 =1,即|m-1|=
=1,即|m-1|=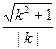 =
=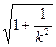 .
.∵|k|∈[
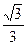 ,
,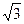 ],
],∴
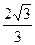 ≤|m-1|≤2.
≤|m-1|≤2.解得
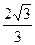 +1≤m≤3或-1≤m≤1-
+1≤m≤3或-1≤m≤1-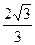 .
.∴m的取值范围是[-1,1-
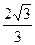 ]∪[1+
]∪[1+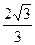 ,3].
,3].(2)可设双曲线方程为x2-
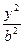 =1(b≠0),
=1(b≠0),由M(
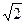 +1,0),A(1,0)得|AM|=
+1,0),A(1,0)得|AM|=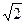 .
.又因为M是△APQ的内心,M到AP的距离为1,
所以∠MAP=
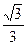 45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1.
45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1.因此kAP=1,kAQ=-1(不妨设P在第一象限),直线PQ的方程为x=2+
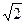 ,
,直线AP的方程为y=x-1.
∴解得P的坐标是(2+
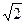 ,1+
,1+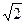 ).
).将P点坐标代入x2-
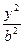 =1得b2=
=1得b2=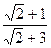 ,
,所以所求双曲线方程为x2-
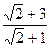 y2=1,
y2=1,即x2-(2
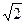 -1)y2=1.
-1)y2=1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

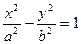 (a>0,b>0)的右准线
(a>0,b>0)的右准线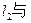 一条渐近线
一条渐近线 交于两点P、Q,F是双曲线的右焦点。
交于两点P、Q,F是双曲线的右焦点。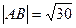 ,求双曲线的方程;
,求双曲线的方程; 和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。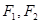 是双曲线
是双曲线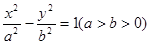 的左、右焦点,
的左、右焦点,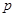 为双曲线左支上一点,若
为双曲线左支上一点,若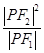 的最小值为
的最小值为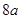 ,则该双曲线的离心率的取值范围是
,则该双曲线的离心率的取值范围是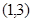
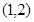
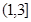
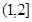
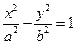 的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.
的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.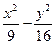 =1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为
=1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为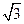 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( )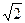 )、(
)、(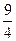 ,5),则双曲线的标准方程为( )
,5),则双曲线的标准方程为( ) ="1"
="1"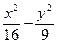 ="1"
="1"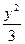 =1,双曲线存在关于直线l:y=kx+4的对称点,求实数k的取值范围.
=1,双曲线存在关于直线l:y=kx+4的对称点,求实数k的取值范围. +
+ =1的焦点为顶点,顶点为焦点的双曲线方程是________________.
=1的焦点为顶点,顶点为焦点的双曲线方程是________________.