题目内容
已知二次函数f(x)=ax2+bx+c,若对一切实数x,f(x)≥f′(x)恒成立,其中f′(x)是f(x)的导函数.(I)求证:f(x)的图象与x轴无交点;
(II)若方程f(x)-2f′(x)=0有两上不同的实数根x1,x2,求证:
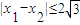 .
.
【答案】分析:(I)由题意因为二次函数f(x)=ax2+bx+c,若对一切实数x,f(x)≥f′(x)恒成立,所以先求二次函数导函数,然后有二次函数求出恒成立时,f(x)的图象与x轴无交点;
(II)先求出函数的导函数,因为方程f(x)-2f′(x)=0有两上不同的实数根x1,x2,等价于对应的二次函数的判别式大于0,利用根与系数的关系即可.
解答:解:(I)∵f′(x)=2ax+b 于是f(x)-f′(x)=ax2+(b-2a)x+c-b
∵对于一切实数x,都有f(x)≥f′(x)恒成立,
故a>0且△1=(b-2a)2-4a(c-b)=b2-4ac+4a2≤0,
于是b2-4ac-4a2<0,
所以f(x)的图象与x轴无交点.
(II)证明:∵f(x)-2f′(x)=ax2+(b-4a)x+c-2b=0有两个不同的实数根x1,x2,
故△2=(b-4a)2-4a(c-2b)=b2-4ac+16a2>0,从而-16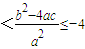 ,
,
有根与系数的关系知: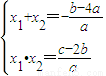 ,
,
∴|x1-x2|2=(x1+x2)2-4x1x2=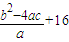 ,于是0<|x1-x2|2≤12,
,于是0<|x1-x2|2≤12,
即|x1-x2|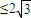 .
.
点评:此题主要考查了二次函数,一元二次方程,一元二次不等式,导数的应用等基本知识,同时考查运算能力以及数形结合,函数思想等数学思想方法.
(II)先求出函数的导函数,因为方程f(x)-2f′(x)=0有两上不同的实数根x1,x2,等价于对应的二次函数的判别式大于0,利用根与系数的关系即可.
解答:解:(I)∵f′(x)=2ax+b 于是f(x)-f′(x)=ax2+(b-2a)x+c-b
∵对于一切实数x,都有f(x)≥f′(x)恒成立,
故a>0且△1=(b-2a)2-4a(c-b)=b2-4ac+4a2≤0,
于是b2-4ac-4a2<0,
所以f(x)的图象与x轴无交点.
(II)证明:∵f(x)-2f′(x)=ax2+(b-4a)x+c-2b=0有两个不同的实数根x1,x2,
故△2=(b-4a)2-4a(c-2b)=b2-4ac+16a2>0,从而-16
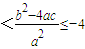 ,
,有根与系数的关系知:
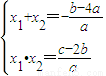 ,
,∴|x1-x2|2=(x1+x2)2-4x1x2=
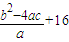 ,于是0<|x1-x2|2≤12,
,于是0<|x1-x2|2≤12,即|x1-x2|
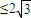 .
.点评:此题主要考查了二次函数,一元二次方程,一元二次不等式,导数的应用等基本知识,同时考查运算能力以及数形结合,函数思想等数学思想方法.

练习册系列答案
相关题目