题目内容

【题目】设双曲线C： (a>0，b>0)的左、右焦点分别为F1，F2，|F1F2|＝2c，过F2作x轴的垂线与双曲线在第一象限的交点为A，已知Q，|F2Q|＞|F2A|，点P是双曲线C右支上的动点，且|PF1|＋|AQ|＞|F1F2|恒成立，则双曲线的离心率的取值范围是(　　)

A. B.

C. D.

【答案】B

【解析】

根据点坐标得到线段|F2Q|和|F2A|，从而得＞，进而有|AQ|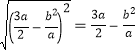＝ ，结合|AF1|＋|AQ|＞|F1F2|，即可求得离心率的范围.

AF2垂直于x轴，则|F2A|为双曲线的通径的一半，

|F2A|＝，A的坐标为，

|AF1|＝.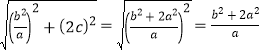

Q，∴|F2Q|＝.

又|F2Q|＞|F2A|＞，

故有|AQ|＝ ；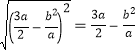

A在第一象限上即在右支上，则有|AF1|＋|AQ|＞|F1F2|，

即＋－＞×2c＞3c7a＞6ce＝＜.∵e＞1，∴1＜e＜.

答案：B

练习册系列答案
相关题目

【题目】设分别为双曲线的左、右顶点，双曲线的实轴长为，焦点到渐近线的距离为．

（1）求双曲线的方程；

（2）已知直线与双曲线的右支交于两点，且在双曲线的右支上存在点，使，求的值及点的坐标．

【题目】设圆的圆心在轴上，并且过两点.

(1)求圆的方程；

(2)设直线与圆交于两点，那么以为直径的圆能否经过原点，若能，请求出直线的方程；若不能，请说明理由.

【题目】已知点,,直线与直线相交于点,直线与直线的斜率分别记为与,且．

（1）求点的轨迹的方程；

（2）过定点作直线与曲线交于两点, 的面积是否存在最大值？若存在,求出面积的最大值；若不存在,请说明理由．

【题目】已知函数f（x）=lnx﹣ ．
（1）若函数f（x）在定义域内不单调，求实数a的取值范围；
（2）若函数f（x）在区间（0，1]内单调递增，求实数a的取值范围；
（3）若x1、x2∈R+ ， 且x1≤x2 ， 求证：（lnx1﹣lnx2）（x1+2x2）≤3（x1﹣x2）．

【题目】泰兴机械厂生产一种木材旋切机械，已知生产总利润c元与生产量x台之间的关系式为c(x)＝－2x2＋7 000x＋600.

(1)求产量为1 000台的总利润与平均利润；

(2)求产量由1 000台提高到1 500台时，总利润的平均改变量；

(3)求c′(1 000)与c′(1 500)，并说明它们的实际意义．

【题目】已知数列{an}中，a1=1，a3=9，且an=an﹣1+λn﹣1（n≥2）．
（ I）求λ的值及数列{an}的通项公式；
（ II）设 ，且数列{bn}的前n项和为Sn ， 求S2n ．

【题目】德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数f（x）= ，称为狄利克雷函数，则关于函数f（x）有以下四个命题： ①f（f（x））=1；
②函数f（x）是偶函数；
③任意一个非零有理数T，f（x+T）=f（x）对任意x∈R恒成立；
④存在三个点A（x1 ， f（x1）），B（x2 ， f（x2）），C（x3 ， f（x3）），使得△ABC为等边三角形．
其中真命题的个数是（ ）
A.4
B.3
C.2
D.1

【题目】已知f（x）=aln（x2+1）+bx存在两个极值点x1 ， x2 ．
（1）求证：|x1+x2|＞2；
（2）若实数λ满足等式f（x1）+f（x2）+a+λb=0，试求λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网