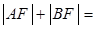题目内容
设F1,F2是双曲线C:
-
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的渐近线方程为______.
| x2 |
| a2 |
| y2 |
| b2 |
如图所示,
不妨设点P在双曲线的右支上.
则|PF1|-|PF2|=2a,又|PF1|+|PF2|=6a,
联立解得
.
∵4a>2a,|F1F2|=2c>2a.
∴∠PF1F2是最小角,因此∠PF1F2=30°.
由余弦定理可得:|PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|cos30°,
∴(2a)2=(4a)2+(2c)2-2×4a×2c•cos30°,
化为c2-2
ac+3a2=0,
∴e2-2
e+3=0,
解得e=
.
∴
=
=
,
解得
=
.
∴渐近线方程为y=±
x.
故答案为:y=±
x.
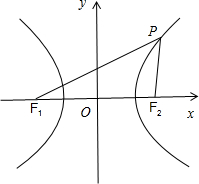
不妨设点P在双曲线的右支上.
则|PF1|-|PF2|=2a,又|PF1|+|PF2|=6a,
联立解得
|
∵4a>2a,|F1F2|=2c>2a.
∴∠PF1F2是最小角,因此∠PF1F2=30°.
由余弦定理可得:|PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|cos30°,
∴(2a)2=(4a)2+(2c)2-2×4a×2c•cos30°,
化为c2-2
| 3 |
∴e2-2
| 3 |
解得e=
| 3 |
∴
| 3 |
| c |
| a |
1+
|
解得
| b |
| a |
| 2 |
∴渐近线方程为y=±
| 2 |
故答案为:y=±
| 2 |


练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
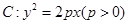 的焦点为
的焦点为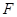 ,
,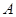 为
为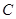 上异于原点的任意一点,过点
上异于原点的任意一点,过点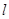 交
交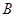 ,交
,交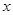 轴的正半轴于点
轴的正半轴于点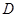 ,且有
,且有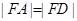 .当点
.当点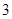 时,
时,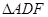 为正三角形.
为正三角形.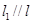 ,且
,且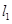 和
和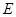 ,
,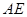 过定点,并求出定点坐标;
过定点,并求出定点坐标;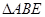 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.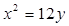 的焦点为
的焦点为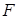 ,经过点
,经过点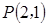 的直线
的直线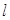 与抛物线相交于
与抛物线相交于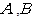 两点且点
两点且点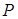 恰为
恰为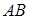 的中点,则
的中点,则