题目内容
(本小题满分12分)
对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[ ]
] ,使
,使 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把 (
( )叫闭函数.
)叫闭函数.
(1)求闭函数 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若函数 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
(1)[-1,1]。(2)函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。(3)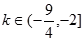 。
。
解析试题分析:(1)根据y=-x3的单调性,假设区间为[a,b]满足,求a、b的值.
(2)取一特殊值x1=1,x2=10,代入验证不满足条件即可证明不是闭函数.
(3)根据闭函数的定义,得到a,b,k的关系式,然后转换为方程有两个不等的实数根来得到参数的范围。
解:
(1)由题意, 在[
在[ ]上递减,则
]上递减,则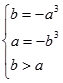 解得
解得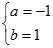
所以,所求的区间为[-1,1]..............................................2分
(2)
取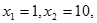 则
则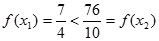 ,
,
即 不是
不是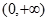 上的减函数。
上的减函数。
取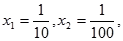
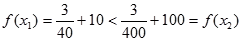 ,
,
即 不是
不是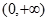 上的增函数,
上的增函数,
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。.............4分
(3)若 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数 的值域为[
的值域为[ ],即
],即 ,
,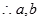 为方程
为方程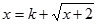 的两个实根,
的两个实根,
即方程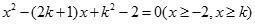 有两个不等的实根。
有两个不等的实根。
当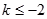 时,有
时,有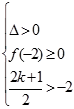 ,解得
,解得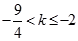 。...............................7分
。...............................7分
当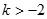 时,有
时,有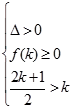 ,无解。........................................10分
,无解。........................................10分
综上所述,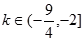 ....................................12分
....................................12分
考点:本试题主要考查了新定义的运用,通过给定的新定义来解题.这种题重要考查学生的接受新内容的能力.
点评:解决该试题的关键是理解闭函数的概念,并能结合所学知识,转换为不等式以及对应的函数关系式。

 为奇函数,
为奇函数,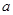 为常数,
为常数, 在区间
在区间 上单调递增;
上单调递增; 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.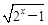 (a>0,a≠1).
(a>0,a≠1).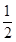 对称,且f′(1)=0.
对称,且f′(1)=0.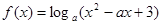
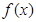 的值域为
的值域为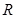 ,求实数
,求实数 的取值范围;
的取值范围; 时,函数
时,函数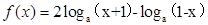 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域;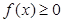 ;
;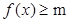 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.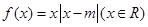 ,且
,且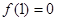 .
.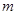 的值,并用分段函数的形式来表示
的值,并用分段函数的形式来表示 ;
;

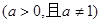
 ;
;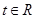 ,不等式
,不等式 恒成立,求
恒成立,求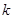 的取值范围。
的取值范围。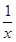 在(0,1)上为减函数.
在(0,1)上为减函数.