题目内容
设a、b是两个非零向量,则“(a+b)2=|a|2+|b|2”是“a⊥b”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
设a、b是两个非零向量,“(a+b)2=|a|2+|b|2”?(a+b)2=|a|2+|b|2+2ab=|a|2+|b|2?a?b=0,即a⊥b;
a⊥b?a?b=0即(a+b)2=|a|2+|b|2所以“(a+b)2=|a|2+|b|2”是“a⊥b”的充要条件.
故选C.
a⊥b?a?b=0即(a+b)2=|a|2+|b|2所以“(a+b)2=|a|2+|b|2”是“a⊥b”的充要条件.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 是两个非零向量,则“向量
是两个非零向量,则“向量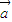 ,
,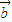 是两个非零向量,则“向量
是两个非零向量,则“向量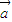 ,
,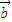 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x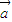 +
+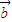 )•(
)•(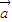 -x
-x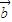 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )