题目内容
(本小题满分12分)
己知圆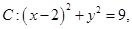 直线
直线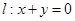 .
.
(1) 求与圆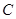 相切, 且与直线
相切, 且与直线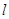 平行的直线
平行的直线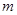 的方程;
的方程;
(2) 若直线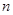 与圆
与圆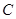 有公共点,且与直线
有公共点,且与直线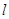 垂直,求直线
垂直,求直线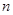 在
在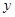 轴上的截距
轴上的截距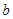 的取值范围.
的取值范围.
己知圆
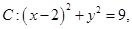 直线
直线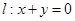 .
.(1) 求与圆
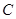 相切, 且与直线
相切, 且与直线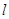 平行的直线
平行的直线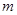 的方程;
的方程;(2) 若直线
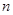 与圆
与圆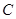 有公共点,且与直线
有公共点,且与直线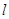 垂直,求直线
垂直,求直线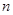 在
在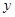 轴上的截距
轴上的截距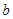 的取值范围.
的取值范围.(1)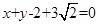 或
或 (2)
(2)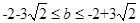
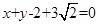 或
或 (2)
(2)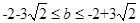
试题分析:解:(1) ∵直线
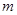 平行于直线
平行于直线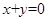 ,
,∴设
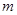 的方程为:
的方程为: 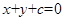 ,
,∵直线
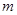 与圆
与圆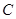 相切,
相切,∴
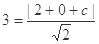
解得
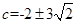
∴直线
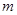 的方程为:
的方程为: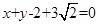 或
或 . ………6分
. ………6分(2) 由条件设直线
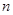 的方程为:
的方程为:
代入圆
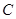 方程整理得:
方程整理得: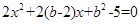
∵直线
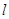 与圆
与圆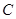 有公共点
有公共点∴
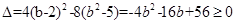 即:
即:
解得:
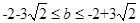 …………………………12分
…………………………12分点评:解决圆的切线方程的一般思路,先结合平行直线系方程设出,利用圆心到直线的距离等于圆的半径得到斜率的值。同理要利用垂直的直线系方程求解表达式,进而得到截距的范围。属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
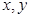 满足
满足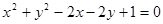 ,
,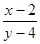 的取值范围为( ).
的取值范围为( ).


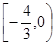
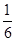 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的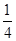 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )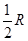 B.
B. 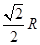 C.
C. 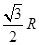 D.
D. 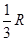
 为何实数,直线
为何实数,直线 与曲线
与曲线 恒有交点,则实数
恒有交点,则实数 的取值范围为 。
的取值范围为 。 与曲线
与曲线 有公共点,则b的取值范围为 。
有公共点,则b的取值范围为 。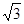 )且与圆
)且与圆 相切的直线方程是 。
相切的直线方程是 。 :
: ,圆
,圆 方程为
方程为
 的值
的值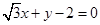 截圆
截圆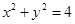 得到的弦长为 .
得到的弦长为 .