题目内容
14.若不等式$\left\{\begin{array}{l}y≥0\\ x-y≥1\\ x+2y≤4\\ x+my+n≥0\end{array}\right.$(m,n∈Z)所表示的平面区域是面积为1的直角三角形,则实数n的一个值为( )| A. | 2 | B. | -1 | C. | -2 | D. | 1 |
分析 先画出满足条件$\left\{\begin{array}{l}y≥0\\ x-y≥1\\ x+2y≤4\end{array}\right.$表示的平面区域,再根据x+my+n≥0表示的平面区域表示为直线x+my+n=0右侧的阴影部分,结合已知中不等式组$\left\{\begin{array}{l}y≥0\\ x-y≥1\\ x+2y≤4\\ x+my+n≥0\end{array}\right.$所表示的平面区域是面积为1的直角三角形,得到满足条件的直线,进而根据直线的方程求出n的值.
解答 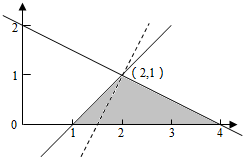 解:满足条件$\left\{\begin{array}{l}y≥0\\ x-y≥1\\ x+2y≤4\end{array}\right.$的平面区域如下图所示:
解:满足条件$\left\{\begin{array}{l}y≥0\\ x-y≥1\\ x+2y≤4\end{array}\right.$的平面区域如下图所示:
由于x+my+n≥0表示的平面区域表示为直线x+my+n=0右侧的阴影部分面积,
故分析可得直线x+my+n=0有2种情况:
①过(2,1)点且与直线直线x+2y=4垂直,解得n=-$\frac{3}{2}$,但由于直角三角形面积为1,不满足题意,故舍去.
②过(2,1)点且与x轴垂直,n=-2,满足直角三角形的面积为1,满足题意;
故选:C.
点评 本题考查的知识点是二元一次不等式(组)与平面区域,根据已知条件分析满足的直线方程是解答本题的关键.

练习册系列答案
相关题目
19.函数f(x)=2x+cos2x在[0,$\frac{5π}{12}$]上的最小值是( )
| A. | -1 | B. | 0 | C. | 3 | D. | 1 |
 如图,已知四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,侧棱AA1⊥底面ABCD,AB=AD=2,AA1=4,M为棱DD1上的一点.
如图,已知四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,侧棱AA1⊥底面ABCD,AB=AD=2,AA1=4,M为棱DD1上的一点.