题目内容
下列命题中:①函数f(x)=sinx+
 (x∈(0,π))的最小值是2
(x∈(0,π))的最小值是2 ;
;②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形:
③如果正实数a,b,c满足a+b>c,则
 +
+
 ;其中正确的命题是( )
;其中正确的命题是( )A.①②③
B.①
C.②③
D.③
【答案】分析:真假命题的判断,一一进行判断.对于①sinx∈(0,1],利用函数的单调性求最小值;对于②等价于2A=2B或2A+2B=180°;对于③构造函数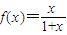 ,证明其在(0,+∞)上为增函数即可
,证明其在(0,+∞)上为增函数即可
解答:解:对于①sinx∈(0,1],不能使用基本不等式求解,故为假命题;对于②由题意2A=2B或2A+2B=180°,故②为真命题;对于③构造函数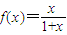 =
=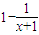 ,从而在(0,+∞)上为增函数,又由a+b>c及即f(a)+f(b)>f(a+b)>f(c)得f(a)+f(b)>f(c)可知为真.故选C.
,从而在(0,+∞)上为增函数,又由a+b>c及即f(a)+f(b)>f(a+b)>f(c)得f(a)+f(b)>f(c)可知为真.故选C.
点评:本题考查内容多,知识综合性强应注意考虑全面,不能顾此失彼.
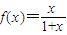 ,证明其在(0,+∞)上为增函数即可
,证明其在(0,+∞)上为增函数即可解答:解:对于①sinx∈(0,1],不能使用基本不等式求解,故为假命题;对于②由题意2A=2B或2A+2B=180°,故②为真命题;对于③构造函数
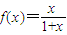 =
=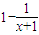 ,从而在(0,+∞)上为增函数,又由a+b>c及即f(a)+f(b)>f(a+b)>f(c)得f(a)+f(b)>f(c)可知为真.故选C.
,从而在(0,+∞)上为增函数,又由a+b>c及即f(a)+f(b)>f(a+b)>f(c)得f(a)+f(b)>f(c)可知为真.故选C.点评:本题考查内容多,知识综合性强应注意考虑全面,不能顾此失彼.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目