题目内容
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用
 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.(1)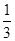 ;(2)
;(2)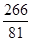 .
.
试题分析:(1)设每次比赛乙获胜的概率为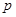 ,则两人比赛五局,乙得一分的概率为
,则两人比赛五局,乙得一分的概率为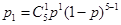 ,乙得一分的概率为
,乙得一分的概率为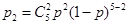 ,因为
,因为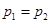 ,所以
,所以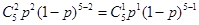 ,即可求得
,即可求得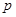 ;
;
(2)由题意比赛进行到有一人比对方多2分或打满6局时停止,所以随机变量ξ的所有可能的取值为2,4,6,利用随机变量的定义及独立事件同时发生的概率公式求出每一个随机变量取值时对应的随机事件的概率,在有离散型随机的期望公式求出期望.
(1)设每次比赛乙获胜的概率为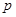 ,则比赛5次乙恰好有
,则比赛5次乙恰好有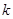 次获胜的概率为
次获胜的概率为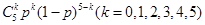 ,
,
由题设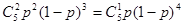 ,且
,且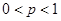 , 化简得
, 化简得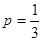 ,
,
所以,乙获胜的概率为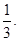
甲获胜的概率为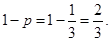
依题意知,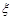 的所有可能值为2,4,6.
的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率为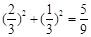 .
.
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从而有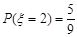 ,
,
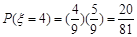 ,
,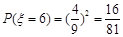 ,
,
故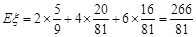 .
.
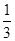 ;(2)
;(2)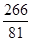 .
.试题分析:(1)设每次比赛乙获胜的概率为
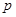 ,则两人比赛五局,乙得一分的概率为
,则两人比赛五局,乙得一分的概率为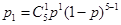 ,乙得一分的概率为
,乙得一分的概率为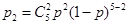 ,因为
,因为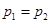 ,所以
,所以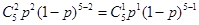 ,即可求得
,即可求得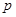 ;
;(2)由题意比赛进行到有一人比对方多2分或打满6局时停止,所以随机变量ξ的所有可能的取值为2,4,6,利用随机变量的定义及独立事件同时发生的概率公式求出每一个随机变量取值时对应的随机事件的概率,在有离散型随机的期望公式求出期望.
(1)设每次比赛乙获胜的概率为
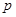 ,则比赛5次乙恰好有
,则比赛5次乙恰好有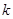 次获胜的概率为
次获胜的概率为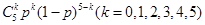 ,
, 由题设
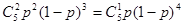 ,且
,且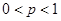 , 化简得
, 化简得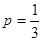 ,
,所以,乙获胜的概率为
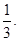
甲获胜的概率为
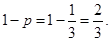
依题意知,
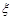 的所有可能值为2,4,6.
的所有可能值为2,4,6. 设每两局比赛为一轮,则该轮结束时比赛停止的概率为
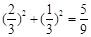 .
.若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从而有
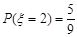 ,
,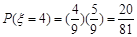 ,
,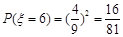 ,
, 故
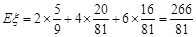 .
. 
练习册系列答案
相关题目
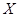 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.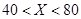
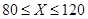
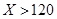
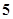 张假钞的
张假钞的 张百元钞票中任意抽取
张百元钞票中任意抽取 张,将其中一张在验钞机上检验发现是假钞,问这
张,将其中一张在验钞机上检验发现是假钞,问这



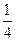 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为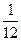 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为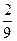 .则丙机床加工的零件是一等品的概率为( )
.则丙机床加工的零件是一等品的概率为( )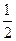
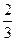
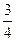
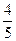


 ,则此次考试成绩不低于120分的学生约有 人.
,则此次考试成绩不低于120分的学生约有 人.