用二分法求方程2x+x-8=0的一个实数解题目和参考答案——青夏教育精英家教网——

题目内容

7．用二分法求方程2^x+x-8=0的一个实数解（精确度0.1）

分析令f（x）=2^x+x-8，易知f（x）在其定义域上连续单调递增，从而取恰当的区间（2.3，2.5），再二分即可．

解答解：令f（x）=2^x+x-8，
易知f（x）在其定义域上连续单调递增，
∵f（2.3）=-0.775＜0，f（2.5）=0.1568＞0；
∴f（x）的零点在（2.3，2.5）上，
又∵f（2.4）=-0.322＜0，
∴f（x）的零点在（2.4，2.5）上，
故方程2^x+x-8=0的一个实数解为2.5．

点评本题考查了方程的根与函数的零点的关系应用及二分法的应用，注意取第一个区间时长度越短，计算量越小．

练习册系列答案

夺冠百分百初中优化测试卷系列答案

新课程问题解决导学方案系列答案

新课程实践与探究丛书系列答案

一课一练创新练习系列答案

北大绿卡课课大考卷系列答案

课时练人民教育出版社系列答案

学海风暴系列答案

金卷1号系列答案

中考考什么系列答案

学法大视野系列答案

相关题目

1．设A₁，A₂是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴的两个端点，P₁，P₂是垂直于x轴的直线与此椭圆的两个交点，M为直线A₁P₁与A₂P₂的交点，求证：点M的轨迹方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1．

18．设a＞0，且a≠1，已知函数f（x）=log_a$\frac{1-bx}{x-1}$是奇函数
（Ⅰ）求实数b的值；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）当x∈（1，a-2）时，函数f（x）的值域为（1，+∞），求实数a的值．

15．函数f（x）=2^x-5x则函数f（x）的零点所在区间可以为（　　）

2．已知是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1的两个焦点，P是椭圆上的一点，若∠F₁PF₂=$\frac{π}{3}$，则△F₁PF₂面积为$\frac{16\sqrt{3}}{3}$．

12．已知函数f（x）=x²-2x，g（x）=ax+2（a＞0），若对任意x₁∈R，都存在x₂∈[-2，+∞），使得f（x₁）＞g（x₂），则实数a的取值范围是（　　）

$（{\frac{3}{2}，+∞}）$

$（{0，\frac{3}{2}}）$

$（{\frac{3}{2}，3}）$

19．若函数$f（x）=\left\{\begin{array}{l}-x+6，x≤2\\ 2+{log_a}x，x＞2\end{array}\right.$（a＞0，且a≠1）的值域是[4，+∞），则实数a的取值范围是（1，$\sqrt{2}$]．

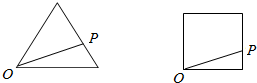如图，点P从点O出发，分别按逆时针方向沿周长均为12的正三角形、正方形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系分别记为y=f（x），y=g（x），定义函数h（x）=$\left\{\begin{array}{l}f（x），f（x）≤g（x）\\ g（x），f（x）＞g（x）\end{array}$考查下列结论：
①h（4）=$\sqrt{10}$；
②函数h（x）的图象关于直线x=6对称；
③函数h（x）值域为$[{0，\sqrt{13}}]$；
④函数h（x）增区间为（0，5）．
其中正确的结论是①②③．（写出所有正确结论的序号）

17．已知函数f（x）=log₂x+2，则方程f（x）-f′（x）=2的根所在的区间为（　　）

（0，$\frac{1}{2}$）

（$\frac{1}{2}$，1）