题目内容
18.设a>0,且a≠1,已知函数f(x)=loga$\frac{1-bx}{x-1}$是奇函数(Ⅰ)求实数b的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)当x∈(1,a-2)时,函数f(x)的值域为(1,+∞),求实数a的值.
分析 (Ⅰ)因为f(x)是奇函数,所以f(-x)=-f(x),进而可得实数b的值;
(Ⅱ)由(Ⅰ)可得函数的解析式,利用导数法,可得函数f(x)的单调区间;
(Ⅲ)由a-2>1得a>3,由(Ⅱ)可得:f(x)在(1,a-2)上单调递减,从而f(a-2)=1,解得答案.
解答 解:(Ⅰ)因为f(x)是奇函数,所以f(-x)=-f(x)…(1分)
从而f(-x)+f(x)=0,即${log_a}\frac{1+bx}{-x-1}+{log_a}\frac{1-bx}{x-1}=0$,
于是,(b2-1)x2=0,由x的任意性知b2-1=0,
解得b=-1或b=1(舍),
所以b=-1.…(3分)
(Ⅱ)由(Ⅰ)得$f(x)={log_a}\frac{x+1}{x-1}$,(x<-1或x>1),
∴${f^/}(x)=\frac{-2}{{({x^2}-1)lna}}$;…(5分)
当0<a<1时,f′(x)>0,即f(x)的增区间为(-∞,-1),(1,+∞);
当a>1时,f′(x)<0,即f(x)的减区间为(-∞,-1),(1,+∞);…(9分)
(Ⅲ)由a-2>1得a>3,…(11分)
所以f(x)在(1,a-2)上单调递减,
从而f(a-2)=1,即${log_a}\frac{a-1}{a-3}=1$,
又a>3,得$a=2+\sqrt{3}$.…(13分)
点评 本题考查的知识点是函数的单调性,对数函数的图象和性质,函数的奇偶性,函数的值域,是函数图象和性质的综合应用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
6.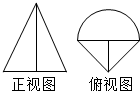 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )| A. | $\frac{π}{2}+1$ | B. | π+1 | C. | $\frac{π}{2}+2$ | D. | π+2 |