题目内容
(本题满分12分)已知等比数列{an}满足a1+a6=11,且a3a4=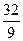 .
.
(1)求数列{an}的通项an;
(2)如果至少存在一个自然数m,恰使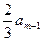 ,
,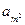 ,am+1+
,am+1+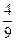 这三个数依次成等差数列,问这样的等比数列{an}是否存在?若存在,求出通项公式;若不存在,请说明理由.
这三个数依次成等差数列,问这样的等比数列{an}是否存在?若存在,求出通项公式;若不存在,请说明理由.
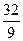 .
.(1)求数列{an}的通项an;
(2)如果至少存在一个自然数m,恰使
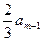 ,
,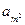 ,am+1+
,am+1+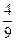 这三个数依次成等差数列,问这样的等比数列{an}是否存在?若存在,求出通项公式;若不存在,请说明理由.
这三个数依次成等差数列,问这样的等比数列{an}是否存在?若存在,求出通项公式;若不存在,请说明理由.(1)an=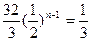 ×26-n或an=
×26-n或an=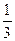 ·2n-1. (2)满足条件的等比数列存在,且有an=
·2n-1. (2)满足条件的等比数列存在,且有an=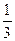 ·2n-1
·2n-1
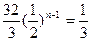 ×26-n或an=
×26-n或an=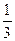 ·2n-1. (2)满足条件的等比数列存在,且有an=
·2n-1. (2)满足条件的等比数列存在,且有an=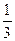 ·2n-1
·2n-1(1)由题意得
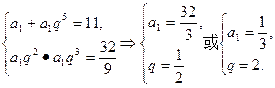
∴an=
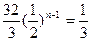 ×26-n或an=
×26-n或an=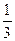 ·2n-1.
·2n-1.(2)对an=
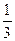 ·2n-1,若存在题设要求的m,则
·2n-1,若存在题设要求的m,则2(
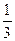 ·2m-1)2=
·2m-1)2=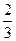 ·
·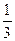 ·2m-2+
·2m-2+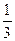 ·2m+
·2m+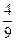 .
.∴(2m)2-7·2m+8=0.
∴2m=8,m=3.
对an=
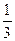 ·26-n,若存在题设要求的m,同理有(26-m)2-11·26-m-8=0.
·26-n,若存在题设要求的m,同理有(26-m)2-11·26-m-8=0.而Δ=112+16×8不是完全平方数,故此时所需的m不存在.
综上所述,满足条件的等比数列存在,且有an=
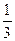 ·2n-1.
·2n-1.
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
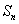 是公差不为0的等差数列
是公差不为0的等差数列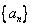 的前
的前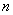 项和,且
项和,且 、
、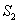 、
、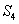 成等比数列。
成等比数列。 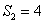 ,求:数列
,求:数列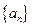 是各项均不为0的等差数列,
是各项均不为0的等差数列,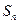 为其前
为其前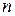 项和,且满足
项和,且满足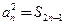 ,令
,令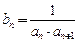 ,数列
,数列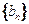 的前n项和为
的前n项和为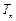 .
.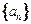 的通项公式及数列
的通项公式及数列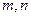
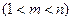 ,使得
,使得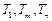 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的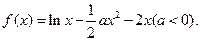
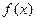 在定义域内单调递增,求
在定义域内单调递增,求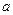 的取值范围;
的取值范围;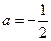 且关于x的方程
且关于x的方程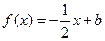 在
在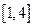 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数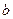 的取值范围;
的取值范围;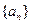 满足:
满足: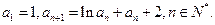 求证:
求证: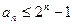
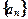 为一等差数列,其中
为一等差数列,其中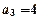 ,
,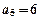 ,
,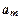
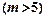 ,使得
,使得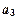 、
、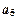 、
、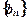 满足
满足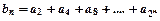 ,求
,求 的公差为
的公差为 ,且
,且 ,若
,若 ,则
,则 为
为 



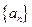 为等差数列,
为等差数列,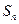 为其前
为其前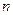 项和,且
项和,且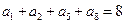 ,则
,则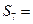



 名,编号为
名,编号为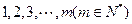 ,该校共开设了
,该校共开设了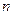 门选修课,编号为
门选修课,编号为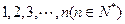 .定义记号
.定义记号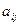 :若第
:若第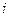 号学生选修了第
号学生选修了第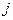 号课程,则
号课程,则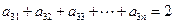 ,则该等式说明的实际含义是3号同学选修了 ▲ 门课程
,则该等式说明的实际含义是3号同学选修了 ▲ 门课程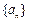 满足
满足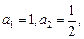 并且
并且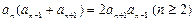 ,则数列的第2010项为( )
,则数列的第2010项为( )


