Question

在半径为13的球面上有A，B，C 三点，AB=6，BC=8，CA=10，则
（1）球心到平面ABC的距离为

 

；
（2）过A，B两点的大圆面与平面ABC所成二面角为（锐角）的正切值为

 

．

Answer 1

分析：（1）由题意说明△ABC是直角三角形，平面ABC是小圆，圆心在AC的中点，利用勾股定理直接求出球心到平面ABC的距离．
（2）如图作出过A，B两点的大圆面与平面ABC所成二面角，直接求出它的正切值即可．

解答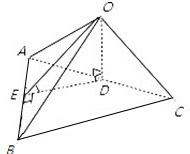：解：（1）AB=6，BC=8，CA=10，△ABC是直角三角形，平面ABC是小圆，圆心在AC的中点D，
AO=13，AD=5，球心到圆心的距离就是球心到平面ABC的距离，
即：OD=12
（2）过D作DE垂直AB于E，连接OE则∠OED就是过A，B两点的大圆面与平面ABC所成二面角．
易得DE=4
所以tan∠OED=

OD

ED

=3
故答案为：（1）12；（2）3．

点评：本题是基础题，考查球的截面问题，二面角的求法，考查空间想象能力，计算能力，能够正确作出图形是解好本题个前提，也是空间想象能力的具体体现．