题目内容
Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,则三棱锥A-BCO的体积是( )
| A、32 | B、64 | C、96 | D、128 |
分析:根据Rt△ABC的三个顶点在半径为13的球面上,得到球心O在三角形ABC上的射影为斜边的中点,然后根据三角形的边长关系求出球的半径,即可求三棱锥的体积.
解答:解: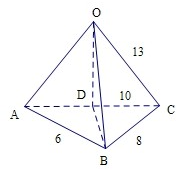 ∵Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,
∵Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,
∴球心O在Rt△ABC的射影为斜边AC的中点D,
即OD⊥面ABC,
设AB=6.BC=8,
则AC=10,CD=5.
∵OC=13,
∴
=12
∴三棱锥A-BCO的体积是
×
×6×8×12=96.
故选:C.
 ∵Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,
∵Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,∴球心O在Rt△ABC的射影为斜边AC的中点D,
即OD⊥面ABC,
设AB=6.BC=8,
则AC=10,CD=5.
∵OC=13,
∴
| 132-52 |
∴三棱锥A-BCO的体积是
| 1 |
| 3 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查三棱锥的体积的计算,利用三角形和球的关系求出三棱锥的高是解决本题的关键.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,则球心到平面ABC的距离是( )
| A、5 | B、6 | C、10 | D、12 |