题目内容
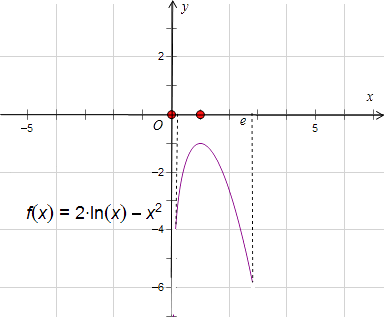
【题目】已知函数f(x)=2lnx﹣x2 , 若方程f(x)+m=0在 ![]() 内有两个不等的实根,则实数m的取值范围是 .
内有两个不等的实根,则实数m的取值范围是 .
【答案】![]()
【解析】解:函数f(x)=2lnx﹣x2 , 若方程f(x)+m=0在 ![]() 内有两个不等的实根, 即函数f(x)=2lnx﹣x2 , 与y=﹣m在
内有两个不等的实根, 即函数f(x)=2lnx﹣x2 , 与y=﹣m在 ![]() 内有两个不相同的交点,
内有两个不相同的交点,
f′(x)= ![]() ﹣2x,令
﹣2x,令 ![]() ﹣2x=0可得x=±1,当x∈[
﹣2x=0可得x=±1,当x∈[ ![]() ,1)时f′(x)>0,函数是增函数,当x∈(1,e)时,f′(x)<0,函数是减函数,
,1)时f′(x)>0,函数是增函数,当x∈(1,e)时,f′(x)<0,函数是减函数,
函数的最大值为:f(1)=﹣1,f( ![]() )=﹣2﹣
)=﹣2﹣ ![]() ,f(e)=2﹣e2 . 函数的最小值为:2﹣e2 .
,f(e)=2﹣e2 . 函数的最小值为:2﹣e2 .
方程f(x)+m=0在 ![]() 内有两个不等的实根,只需:﹣2﹣
内有两个不等的实根,只需:﹣2﹣ ![]() ,
,
解得m∈ ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
